Worksheet #10 - PHY102 (Spr. 2005)

The wave and diffusion equations

Due Thursday 7th April

In this worksheet we will study two partial differential equations that are very important in physics.

Many wave motions can be described by the linear wave equation. We shall do problems concerning waves on a string, but the equation we study has many other applications. For example atomic vibrations in solids, light waves, sound waves and water waves are all described by similar equations. The linear wave equation for the waves on a string is the partial differential equation,

$$\frac{1}{v^2}\frac{{\partial^2}y(x,t)}{{\partial}t^2}= \frac{{\partial^2}y(x,t)}{{\partial}x^2},$$ (1)

where y(x,t) is the distance by which the string is displaced at location x, at time t. $v=(T/\mu)^{1/2}$ is the wave speed and is related to the tension T and mass density $\mu$ of the string(see Halliday and Resnick for the derivation).

A second partial differential equation that is very important in physics is the diffusion equation. Atoms in a gas diffuse around in a manner described by this equation. Similarly pollutants in the ground often diffuse through the soil. This motion is very different than wave motion. In general each physical system has ranges of parameters where the motion is ``diffusive'' or ``wavelike''. In solids for example motion is wavelike at short times and over long distances (e.g. sound waves), but diffusive on long times and short distances (atomic hops). The diffusion equation is given by,

$$\frac{{\partial}c(x,t)}{{\partial}t}=D\frac{{\partial^2}c(x,t)}{{\partial}x^2}.$$ (2)

Here c(x,t) is the concentration of diffusing atoms at position x at time t. Here you can imagine putting a drop of ink in water and watching the color spread. In that case, c(x,t) is the density of ink. D is the ``diffusion constant'' which sets the rate at which the spreading occurs.

Problem 1 - Wave Phenomena

(i) Standing waves. Consider waves on a string of length L=1. The transverse displacement at each end of the string is fixed at zero. Check that the two solutions: $y1(x,t)=y_m Sin(kx-{\omega}t)$ and $y2(x,t)=y_m Sin(kx+{\omega}t)$, satisfy the wave equation. If we seek the ``fundamental mode'', how are kand $\omega$ related to v and the length of the string? Set k=k₀ and $\omega=\omega_0$ (ie. the values for the fundamental) and show that y(x,t)=y1(x,t)+y2(x,t) gives rise to standing waves. Animate the solution y1and the solution y. Show your animation to a TA (don't try to print it out)

(ii) Beats. Now consider two solutions of the form $y1(x,t)=y_mCos(kx-{\omega}_1t)$, and $y2(x,t)=y_mCos(kx-{\omega}_2t)$, where $\omega_1 = \omega + \delta \omega$ and $\omega_2 = \omega - \delta \omega$ Check that the linear superposition of these two propagating waves produces a beat pattern. How does the beat frequency depend on $\delta \omega$?

(iii) Superposition. Almost all functions can be written as a superposition of sine and cosine waves. As an example, consider the linear superposition of sine waves such that;

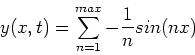$$y(x,t)=\sum_{n=1}^{max}-\frac{1}{n}sin(n x)$$ (3)

Check the evolving pattern as max is increased. Make plots of y(x,t) for max =3, 10, 100 terms. Can you identify the curve as max becomes large.

Problem 2 - Diffusion.

Check that $c(x,t) = \frac{1}{\sqrt{2Dt}}exp(-\frac{x^2}{4Dt})$ satisfies the diffusion equation. Animate the plots of c(x,t) for different values of t. Notice that the amplitude of c(x,t) decays with time, this is the essence of ``diffusion''. In contrast, in the linear wave equation, the wave amplitude remains constant, it propagates instead of spreading. In reality there is some ``damping'' of waves, and this is modeled by adding a ``diffusion term'' to the wave equation (like the ``damping term'' we sometimes add to Newton's equation). Show a TA your animation, but don't try to print it out