


Next: About this document ...
Worksheet #9 - PHY102 (Spr. 2005)
Due March 31st 2005
More on ``Do loops'', Illustrating Chaos
Tools that you need
You will need the following this week (look them up in the online help):
Do (you can also use Table or NestList)
You will also need to learn how to plot lists of numbers using:
ListPlot
In addition, you need to recall that animation is
very simple in mathematica. Simply generate a series of
frames (e.g. using a ``Do'' loop) and then double click on one of the
frames. This automatically animates the set of frames.
The new physics - Chaos
Chaos, though discussed extensively for a couple of
centuries (e.g. Boltzmann and Maxwell discussed ``molecular
chaos''), it has really come into its own since the
widespread use of computers. An early surprise is that
even quite simple looking systems can have chaos, whereas
it was originally thought that chaos only
occured in systems with billions of molecules. In this
worksheet you will study perhaps the simplest
system which shows chaos, namely the ``mapping''
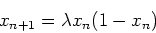 |
(1) |
This mapping models, for example, how a population
density, xn+1, changes as a function of the number of
generations, n. Actually, it is not a very realistic model
but it does illustrate many of the features of more
complex systems. The parameter 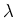 can be considered
to be the ``birth rate'', ie. the number of offspring from the
last generation. Anyway the way it works is that
if we know the population density at some time and
call that density x0, then the population density
of the next generation is
can be considered
to be the ``birth rate'', ie. the number of offspring from the
last generation. Anyway the way it works is that
if we know the population density at some time and
call that density x0, then the population density
of the next generation is
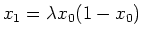 . This
procedure is continued using Eq. (1) to find the
population density for later generations. Intuitively,
chaos means lack of order. Mathematically, it is defined
by how stable the behavior of a set of equations is to
small perturbations in the initial conditions. In the
context of equation (1) this means, how stable are the
set of iterates
(x0,x1,x2,x3...) when
you make the small change
. This
procedure is continued using Eq. (1) to find the
population density for later generations. Intuitively,
chaos means lack of order. Mathematically, it is defined
by how stable the behavior of a set of equations is to
small perturbations in the initial conditions. In the
context of equation (1) this means, how stable are the
set of iterates
(x0,x1,x2,x3...) when
you make the small change
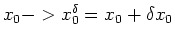 . If this
change is made, we get a new set of iterates
. If this
change is made, we get a new set of iterates
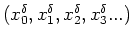 .
If a set of equations is in a chaotic regime then
the divergence of trajectories is exponential with
a positive ``Lyapunov'' exponent. In the context of
our example,
.
If a set of equations is in a chaotic regime then
the divergence of trajectories is exponential with
a positive ``Lyapunov'' exponent. In the context of
our example,
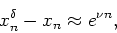 |
(2) |
where the Lyapunov exponent, 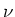 , is positive.
, is positive.
Problem.
(i) Write a Mathematica code to iterate the mapping
(Eq. 1). Plot the steady state behavior of the
mapping as a function of the parameter 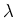 for
for
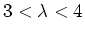 .
.
(ii) In the regime in which ``looks chaotic'' in
your graph, obtain an estimate of the Lyapunov
exponent using Eq. (2).



Next: About this document ...
Phil Duxbury
2002-03-15
![]() for
for
![]() .
.