Interactive guide to diffraction ..

Interactive Tutorial about Diffraction
Basic example III: Row of atoms

Basic examples
Single atom
Pair of atoms
Row of atoms

Interactive examples
1D crystal builder
Polygons of atoms
Different atoms
Ewald sphere
Units
Interference
Bragg's law

Goto
Contents

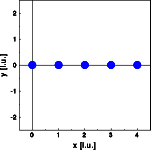
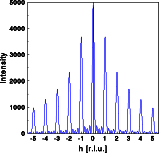
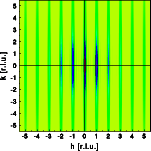
In this last basic example we calculate the Fourier transform of a small 1D crystal, i.e. a row of five silicon atoms parallel to the x direction. Again, the scattering factors for X-rays are used. The pictures below show the crystal structure and the corresponding 1D and 2D Fourier transform. Click on the pictures to get a full screen version.

The middle image shows a one dimensional cut through reciprocal space parallel to the row of atoms, while the right image shows a two dimensional cut through reciprocal space. Perpendicular to the row of atoms the intensity falls off continuously with increasing scattering vector. Parallel to the row of atoms the intensity is modulated. The "Bragg" reflections are sharper than in the previous example. Despite the small number of atoms the subsidiary maxima are hardly visible.

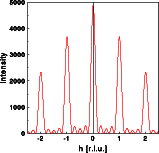
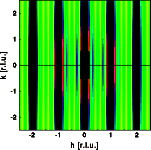
By calculating only the inner section of reciprocal space students can observe the subsidiary maxima much better. You can see that there are n-1 minima and n-2 maxima, where n is the number of atoms in the row. In the 2-D plot the "Bragg" disks are heavily overexposed (enlarged by factor of 10) to make the subsidiary maxima visible.

Again use the interactive simulations and compare the results for neutron and X-ray scattering, or change the number of atoms making up the simulated crystal.