ISP 205, Section 3, Spring 1997

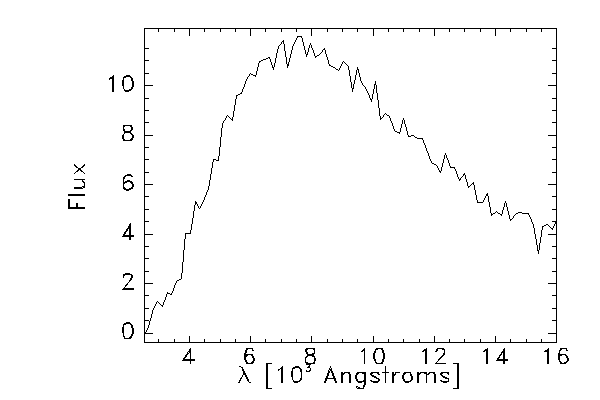
Homework 6: Stars

Due: Thursday, 13 March 1997 (at the beginning of class) 

                                        Name: ________________________


                                        Student Number: ______________
1. (10 pts) Thermal Radiation
Calculate the temperature of the surface of Arcturus. The observed radiation from Arcturus is shown on the graph below of Flux vs. Wavelength. (The formula to use is Wien's Law, section 13.1 of your book.) SHOW YOUR WORK!!
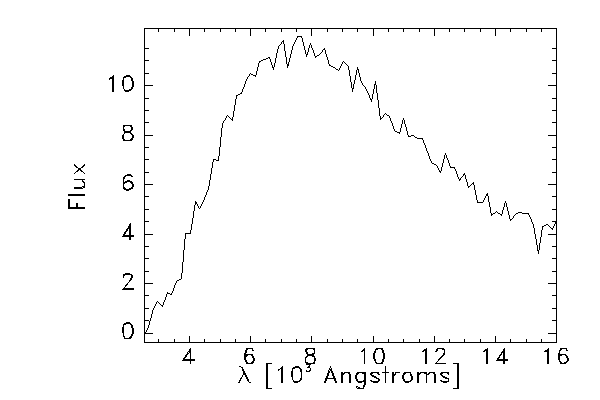
We suggest the following approach to this problem:
  1. Find and write down the formula.
  2. Solve the equation for the algebraic symbol asked for, in this case Temperature.
  3. Determine the values of the variables in the equation that are known. From the graph determine the value of the wavelength of the maximum radiation.
  4. Plug the values of the known variables into the formula and do the math to solve for the unknown variable. Remember units.
  5. Does your answer make sense to you? Check it with the value from your list of 16 brightest stars. 


   lambda = 3x107 / T [K] Angstroms

   T [K]  = 3x107 / lambda Angstroms

          = 3x107 / 7.5x103 Angstroms

          = 4x103 K 

          = 4000 K

This is much cooler than the Sun's temperature of 5750 K, as one would expect 
for a red giant like Arcturus.
2. (12 points) Parallax
Astronomers have measured the parallax of the star "gamma ISP" to be 1 arcsecond. What is its distance from the Sun in parsecs and in Light Years? SHOW YOUR WORK! See section 3.3 (pp 37-38), p 74 and pp 89-90, in the text for a discussion of measuring distance using parallax.


The formula on page 90 is 

	D = 57.3[o] X A [AU]/p [degrees]

        D = 57.3o X 1 AU / 1 arcsec

        D = 57.3o X 1.5x108 km / 0.0002778 arcsec

        D = 57.3o X 1.5x108 km / 0.0002778o

        D = 57.3o X 1.5x108 km / 0.0002778o

	D = 3.1 x 1013 km

	D = 3.26 Light-years

	D = 1 parsec 

		OR

You could use the formula given in class where we already did the conversions
for you:  

	D [parsec] = 1 / p [arcsec]

	D = 1 parsec
Look in appendix E "Stars Nearer than 4 Parsecs" for the star closest to the Sun. How does the distance to "gamma ISP" compare to this star?

If a star with a parallax as large as "gamma ISP's" did exist, it would be the closest star to the Sun.

Which stars, from your list of 16 brightest northern hemisphere stars, are closer to the Sun than 4 parsecs?

Of the brightest stars, only Sirius and Procyon are closer to the Sun than 4 parsecs. Both are binaries. Even they have such a small parallactic shift, the ancient Greeks could not measure it. What is the significance of the closest stars not being the apparent brightest ones?

3. (16 pts) Hertzsprung-Russell (HR) Diagram
On the Hertzsprung-Russell (HR) diagram below plot points representing the Luminosity and Surface Temperature of the 16 brightest stars in the Northern Hemisphere from your list. The values of the luminosity [in units of the Sun's luminosity (LSun)] and the surface temperature for each star are given on your list. Label each star with its name.
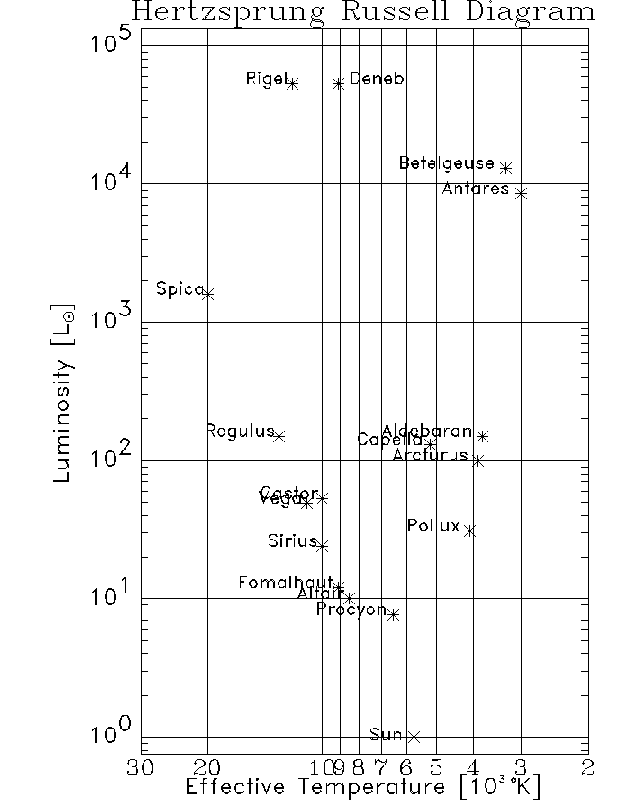
4. (5 pts) Using the HR Diagram you just constructed, the largest of the followi ng stars is:
(a) Procyon
(b) Pollux
(c) Betelgeuse
 (d) Spica
(e) Antares

5. (5 pts) Fomalhaut and Deneb emit the same amount of radiation from each square meter of their surface, but Deneb is more than 1000 times more luminous than Fomalhaut. The reason is:

Deneb must have a 1000 times more surface area from which to emit light as Fomalhaut. That is, it's bigger in size.

6. (16 pts) Classifying Stellar Spectra
Do Discovery 14-1 from pages 313-315 in your textbook. That is, classify the spectral types for the 8 stars in figure 14-1-1, using the comparison spectra in figure 14-2, and fill in the types in the table below. [Do NOT do discovery inquiries 14-1a and 14-1b.]


          STAR                SPECTRAL TYPE

          eta Dra             G8

          alpha Lyr (Vega)    A0

          beta Cas (Caph)     F2

          alpha Aur (Capella) G8

          alpha Sco (Antares) M1

          alpha Per (Mirfak)  F5

          epsilon Per         B1

          gamma Boo           A5

Notice how the hydrogen and calcium lines compare 
to each other as the stellar temperature changes.  (You do not need to
memorize the temperature correspondence to the letters.)

Visions of the Universe

Beth Hufnagel's home page, email: hufnage4@pilot.msu.edu
Bob Stein's home page , email: steinr@pilot.msu.edu