Kirchoff's laws / RC Circuits Examples

Example #1

Problem:

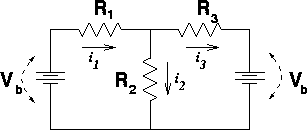
Find the currents through all the resistors in the circuit below:

DATA: V_b = 12 V, R₁ = 10 W, R₂ = 15 W, R₃ = 20 W

Solution:

Summing the voltages around the left and right loops gives the following two equations:

where i₃ has been replaced by i₁ - i₂. Multiplying Eq. (1) by R₃, multiplying Eq. (2) by R₁, then adding the equations yields:

which rearranged yields

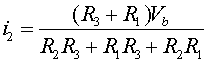     Once i₂ is known, Eq. (1) can be used to get i₁, and i₃ can be found as the difference i₁ - i₂.

i₂ = 0.554 amps, i₁= .369 amps, i₃ = -.185 amps

Example #2

Problem:

Find the charges on all the capacitors in the circuit below:

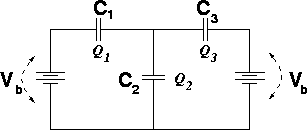
DATA: V_b = 12 V, C₁ = 10 mF, C₂ = 15 mF, C₃ = 20 mF

Solution:

Summing the voltages around the left and right loops gives the following two equations  

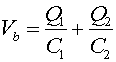
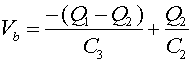
where Q₃ has been replaced by Q₁ - Q₂. Dividing Eq. (1) by C₃, dividiing Eq. (2) by C₁, then adding the equations yields:

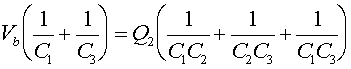
which rearranged yields

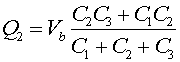
     Once Q₂ is known, Eq. (1) can be used to get Q₁, and Q₃ can be found as the difference Q₁ - Q₂.

Q₂ = 120.0 mC, Q₁= 40.0 mC, Q₃ = -80 mC

Example #3

The circuit below has been in position a for a long time. At time t = 0 the switch is thrown to position b. DATA: V_b = 12 V, C = 10 mF, R = 20 W

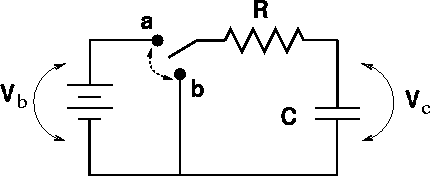
a.) What is the curnent through the resistor just BEFORE the switch is thrown?

I = 0

b.) What is the current through the resistor just AFTER the switch is thrown?

Solution: I = V/R

I = 0.6 amps

c.) What is the charge across the capacitor just BEFORE the switch is thrown?

Solution: Q = CV

Q = 120 mC

d.) What is the charge on the capacitor just AFTER the switch is thrown?

Solution: Charge does not change instantaneously.

Q = 120 mC

e.) What is the charge on the capacitor at at time t = 0.3 msec after the switch is thrown?

Solution: Q = Q₀exp(-t/t) , where t = RC = 0.2 msec

Q = 26.8 mC

Example #4

Considering the same circuit, only with the switch thrown from b to a at time t = 0 after having been in position b for a long time. DATA: V_b = 12 V, C = 10 mF, R = 20 W

a.) What is the curnent through the resistor just BEFORE the switch is thrown?

I = 0

b.) What is the current through the resistor just AFTER the switch is thrown?

Solution: I = V/R

I = 0.6 amps

c.) What is the charge across the capacitor just BEFORE the switch is thrown?

Solution: Q = CV

Q = 0

d.) What is the charge on the capacitor just AFTER the switch is thrown?

Solution: Charge does not change instantaneously.

Q = 0

e.) What is the charge on the capacitor at at time t = 0.3 msec after the switch is thrown?

Solution: Q = Q₀(1.0 - exp(-t/t)) , where t = RC = 0.2 msec

Q = 93.2 mC

Kirchoff's laws / RC Circuit's index