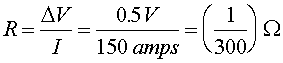
Examples for Resistors
Example #1
Problem:
A wire of length L = 60 m needs to be laid to carry a current of 150 amps with a voltage drop of no more than 0.5 V. The wire is to be made of copper which has a resistivity r = 1.72E-8 Wm. What is the minimum diameter D of the wire?
Solution:
The resistance of the wire needs to by less than the voltage drop divided by the current.
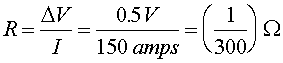
The resistance is given by R = rL/A, therefore the cross sectional area is:
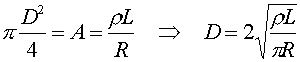
D = 1.99 cm
Example #2
Problem:
Consider the circuit below. What is the equivalent resistance Rab?
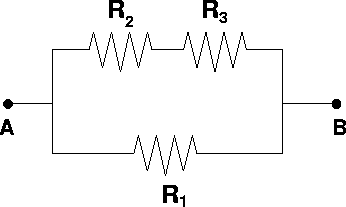
DATA: R1 = R2 = R3 = 7.0 W
Solution:
First consider the upper two resistors as a single resistor, R23. The resistance RAB can be found by adding R1 and R23 in parallel.
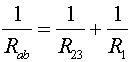
Adding one 1/14 and 1/7 gives 3/14, therefore
RAB = (14/3) W
Example #3
Problem:
What is the equivalent resistance RAB of the three resistors shown below.
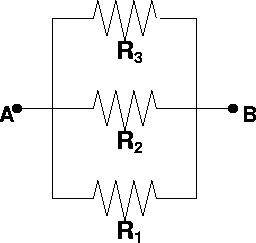
Data R1 = R2 = R3 = 6 W.
Solution:
Use the relation 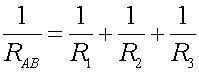 to solve for RAB.
to solve for RAB.
RAB = 2 W
Example #4
Problem:
A 12-volt battery is used to heat a 120 ml cup of coffee by submerging an 8.0-ohm resistor. How long will take to bring the coffee from 20 oC to 100 oC?
Solution:
The energy needed to heat the water is:
![]()
where Cv is the specific heat, one calorie per gram, DT is the change in temperature and m is the mass, 120 g. One then obtains the energy, E = 9600 calories = 4.03E4 J. The time Dt can be found by
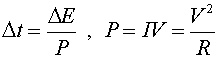
Dt = 37 minutes