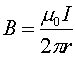one can solve for I.Examples for Magnetic field sources
Example #1
Problem:
A magnetic field of magnitude 1.30E-3 T is measured a distance of 3.0 cm from a long straight wire. What is the magnetic field of the wire?
Solution:
Using 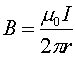one can solve for I.
I = 195 amps, quite a current!
Example #2
Problem:
a.) Two wires carry currents in the same direction as shown below. Where are the points where the magnetic field is zero?
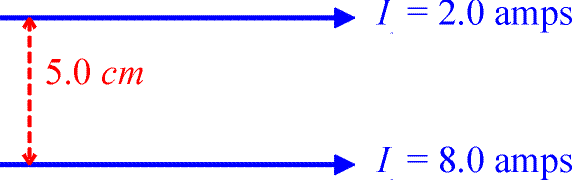
Solution:
Using the right-hand rule, will convince one that the magnetic field contriubtions from the two wires only cancel in the region between the wires. One must find a position that is four times closer to the upper wire, which would be one cm below the upper wire. Using algebra to come to the same conclustion, consider a point located a distance y below the upper wire.
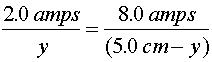
Solving for y gives the 1.0 cm answer.
1.0 cm below the upper wire
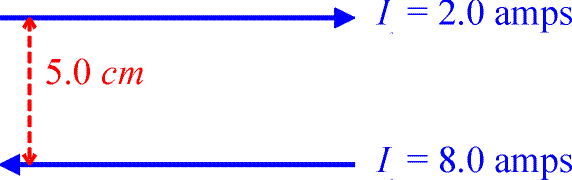
b.) Now consider two wires carrying currents in the opposite direction as shown below. Where are the points where the magnetic field is zero?
Solution:
Using the right-hand rule again, allows one to see that the magnetic-field contributions from the two wires have opposite signs either above or below the wires, but not between them. Of course when you are below the lowere wire, the upper wire can never cancel out the lower wire's contribution since the lower wire carries more current and is closer to you. Therefore consider a point a distance y above the upper wire.
Solving for y,
1.67 cm above the upper wire
Example #3
Problem:
What is the force felt by the square loop shown below due to the current in the long wire?
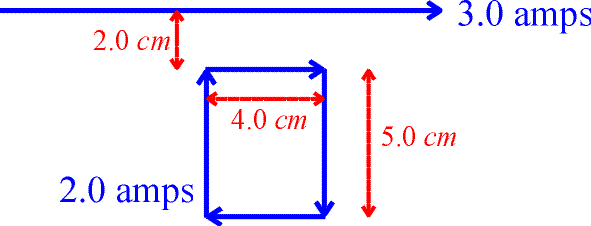
Solution:
There is no net contribution from
the two vertical segments of the rectangular loop since the
currents are in opposite directions. Using 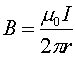with r
= 2.0 cm and = I = 3.0 amps, one can solve for the magnetic
field at the upper segment of the rectangular loop due to the
long wire. One can then find the force on the upper segment, F
= ILB, with L
= 4.0 cm and I
= 2.0 amps. The
force on the upper segment is upwards toward the long wire
because the currents are in the same direction. Repeating the
steps for the bottom wire which is located a distance r
= 7.0 cm from the long wire, allows one to calculate the
force on the lower segment or the rectangle. This force points
down, but is obviously smaller in magnitude than the force on the
upper segment. Adding the forces gives the answer.
F = 1.71E-6 N
Example #4
Problem:
A long cylindrical solenoid with 200 turns/cm carries a current of 4.0 amps. The diameter of the solenoid is 0.4 cm and the length is 8.0 cm and the mass of the moon is 7.35E22 kg. What is the magnetic field inside the solenoid?
Solution:
The magnetic field only depends on the current (I = 4.0 amps) and the number of turns per unit length (N/L = 200).
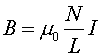
B =0.1005 T