• Describe how optical images are formed by mirrors and simple lenses by the reflection and refraction of light
• Learn how to form an image experimentally and determine its position and size
• Use a ray diagram to determine the position and size of the image
• Use an equation to determine the position and size of the image
• Compare the results of these three techniques

Introduction:
In the real world there are relatively few systems capable of forming and recording images of objects which emit or reflect light. The eye (plus brain) is the oldest. It was followed by still and movie cameras which use light sensitive film and quite recently by still and video cameras which use a light sensitive semiconducting array to produce the image. Any one of these imaging devices may be connected to a microscope, telescope or pair of binoculars which itself captures the light and may form its own image which is then used as the object, or source of light for the final image. All of these systems use mirrors and/or single or combinations of lenses.

Assuming a given source of light, an object, the questions we want to answer are:

   What determines the position of the image?

   What determines the size of the image?

   What determines whether the image is upright or inverted as compared with the object? (See Question 1)

   Can we define an image if the rays from the object are not "focused to some set of points in space"? (See Question 2)

Question 1: Ask yourself if you could ever know whether the image of the streetlight on your retina is upright or inverted.

Question 2: When you see yourself in a mirror, you appear to be behind it, but, of course you aren't. The mirror has somehow formed an image that your eye interprets as "you behind the mirror". Why does your eye think it sees you there?

Concepts for a single lens:
There are many optical systems we could study but since we have only three hours in laboratory, we will limit ourselves to a single lens or a pair of lenses which are thin and rather close to one another. In preparation for this experiment you should read Section 35-6, Thin Lenses, in "Fundamentals of Physics" (Part 4) by Halliday, Resnick and Walker.

The most useful way to approach how lenses (or mirrors) form images using light which comes from an object is to think that the light travels in a straight line in the form of a ray until it is refracted by a lens (or reflected by a mirror).

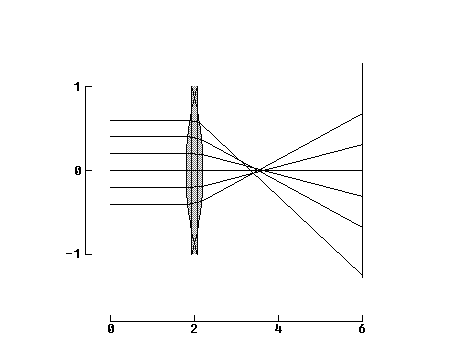
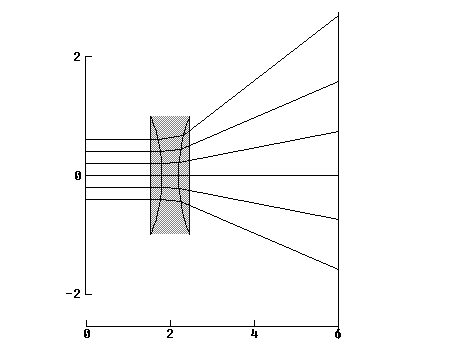
      Fig 1a Convex lens                 Fig 1b Concave lens

Note:There are three "rules" about rays which let you form images using them:

    a. Any ray which comes in to the lens along a path parallel to the axis passes through the focal point, f.

    b. Any ray which comes to the lens at its center passes through it without deviating from its original path.

    c. Any ray which passes through the focal point on its way to the lens leaves the lens parallel to the axis

If we place a source of light (an object) which has a height O, a distance p from the lens, the image will have a height I and be a distance i from the lens (Fig 2).

There are two important equations which relate these quantities:

The thin lens equation which relates the focal length to the image and object distances:

  Eqn 1

The magnification equations which relates the heights (or widths) of the object and image - lateral magnification:

         Eqns 2a and 2b

Exercise 1. Using Fig 2 and the idea of similar triangles, show that Eqns 2a and 2b are equivalent.

Fig 2 Convex Lens with object and image

Procedure:

1. Holding one of the converging thin lenses in your hand, form an image of a "far away" object on a piece of paper (or your partners hand) and obtain a value for f of that lens.
2. Place the object and the screen on the optic bench quite close together (~30cm apart). Using the same lens try to place it between them to form an image on the screen. If you are unable to do it, move the screen farther away until you can form an image. Measure p, i, O and I and determine how your measured numbers agree with what you calculate using Eqns 1 and 2. Make a table for your data and calculations with columns for p, i, O, I, f, m_exp and m_calc . Include columns for errors in these quantities. (See Note just below.)

Note: The errors in these quantities are really experimental and arise from:

• a. Your inability to determine when the image is "perfect".

• b. The fact that the lenses form images at slightly different places depending on the wavelength of the light and whether it comes in near the center or near the edge of the lens. Since white light consists of many wavelengths and the comes into the whole lens, both of these effects are sources of errors.

Question 3. What is the minimum separation between object and screen at which you can form an image? See if you can calculate this from Eqn 1.

• Move the screen till it is quite far from the object and move the lens to form a new image. Measure the parameters and determine how they compare with the calculated values.
• Attempt to form another image by moving only the lens — do the parameters again.

Question 4. How are the image and object distances and the magnification related for the two images?

• As the last experiment with a single converging lens place the object so that p < f and look for an image — which you wont find. Insert p and f into Eqn 1 to obtain i.

Question 5. What words does one use to describe the images in the two cases i > 0 and i < 0 ?

Concepts for a pair of lenses:
The image of a single object formed by two lenses "in series" can be thought of in the following fashion; Lens #1 forms image #1 from object #1 with all the usual equations and conditions determining p₁, i₁, O₁, I₁, and m₁. Image #1 becomes the object for lens #2 with the object distance p₂ being the distance from i₁ to lens #2. It forms a second image with the usual parameters p_2, i_2, O₂, I₂, and m_2. The only different result is that the total magnification m_t = m_1* m₂

Procedure:
1. Place a convex lens with f = 15 cm (lens #1) quite close to the light source and search for an image by moving the screen. Place a second convex lens (lens #2) on the bench and search for an image now. If all the numbers are o.k. you will not find an image with a single lens but with two. Make a table for all the parameters and errors (there are lots of them) and decide which you can measure and which you have to calculate. In the end, you will compare the measured total magnification m_t = I₂/O₁ with that calculated from m_t = m₁*m₂.

2. Using a concave lens for lens #1, and a convex lens for #2 do exactly the same experiment again. You will have to ask your TA for the focal length of #1.