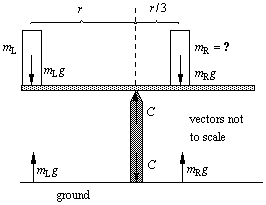
HW 7: Ch. 7, Prob. 1-28, (correct numbering 18+) skip 21 "Which force ...." (Do not guess the value of mR, or mL! Use the subscripts L and R on the masses)

1. The weights are WL = mLg and WR = mRg

2. The compression forces are: CL = mLg and CR = mRg, the directions (are) the same.

The forces acting on the board and on the earth are drawn on the Figure.

3 The force angles are 90°

4. Magnitude of torques about the pivot point are: tL = mLgr and, tR = mRgr/3

5. The torque vectors try to rotate the board in the ( opposite) directions

6. Mass mL generates the torque vector , tL = –mLgr

7. Mass mR generates the torque vector , tR = +mRgr/3

8. Net torque vector , acting on the board, tNet =. –mLgr + mRgr/3

9. The net torque on the board must be, tNet = 0 , if the board is balanced.

10 The right mass, mR = 3mL

–mLgr + mRgr/3 = 0
mR/3 = mL
mR = 3mL

11. The net force on the board must be, FNet = 0 , if it is balanced.

12. The net force acting on the board, ( CL = –mLg, CR = –mRg = –3mLg )

FNet, = CL + CR + C = (–mLg )+(– 3mLg)+(+C) = 0 (balanced)

13. The magnitude C = 4mLg .

The forces acting on the ground (do) balance

14. If the masses are hung from the board, the C's change to T's and nothing else.

15. The net force and net torque must be set equal to zero to determine the forces acting on a balanced beam

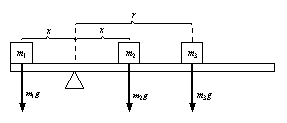
16. The force vectors applied to the board are shown on the Figure and generate torques:

17 t1 = –m1gx , t2 = +m2gx , and , t3 = +m3gx (+, clockwise)

18. Net torque vector tNet = t1 + t2 + t2 = –m1gx +m2gx +m3gx

19. A balanced board has a net torque vector = 0 = –m1gx +m2gx +m3gr

m3gr = (m1g – m2g )x

r = [(m1 – m2 )/ m3]x

20. The location, r , of m3 that will balance the board is a) r = [(m1 – m2 )/ m3]x

Figure for problems 22-25

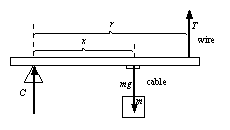
22. r = 10 m , m = 100 kg, , x = 7 m ,

(C at the pivot, F in the cable (use m ) , and T in the wire) are drawn on the Figure.

23. The torque vectors acting on the board are:tpivot = 0 , tcable = mgx , twire = –Tr.

tNet = mgx – Tr = 0 T = mgx/r

24. The tension in the wire is, T = mgx/r= (100 kg)(10 N/kg)(7 m)/(10 m) = 700 N

FNet, = C + T + F = (+C ) + (+mgx/r) + (–mg) C = mg( 1– x/r ) = (1000 N)

25. Cpivot = mg( 1– x/r ) = (1000 N)[ 1– (7 m)/(10 m)] = (1000 N)(0.3) = 300 N

T = F (balance at the handle)
TB = 2T = 2F (balance at the pulley)
Ff = TB= 2F (balance at the mass)
Ff = +2F (same direction as F)
Fwall = 3T = 3F (same direction as F)
Fwall = +3F

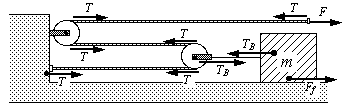
26. The tension in the rope is: a) F   b) 2F   c) F/2   d) 3F   e) 3F/2

27. The frictional force vector is:a)Ff = 0,   b) Ff = +F,   c) Ff = –F,   d) Ff = –2F,   e) Ff = +2F

28. The net on the wall is: a) Ff = +F,   b) Ff = –F,   c) Ff = –2F,   d) Ff = +2F,   e) Ff = +3F
Back to Homework List