1. Which force(s), electromagnetic(E), gravitational(G), weak nuclear(WN) or strong nuclear(SN), is(are) primarily responsible for the following (100% correct for credit):
color of TV screen. E thinking about life. E
exposure of photo film. E  measuring speed by radar. E
clotting of blood to a scab. E measuring speed by laser. E
decay of a neutron to proton+e+n WN  location of the rings of Saturn. G
microwave heating . E bending of light by a prism. E
spoiling of milk. E  floating of helium-filled balloon . E & G
2. External force vectors act on an object:. F1 = +3mg, F2 = +5mg, F3 = –2mg, and F4,
If the external forces balance, what is F4?
a) F4 = –10mg,   b) F4 = +8mg,   c) F4 = –8mg,   d) F4 = –6mg   e) F4 = +6mg

3. A mass weighs 100 N on the planet Kongo (gKongo = 2.5 N/kg). What is its weight on the Earth? gKongo = 2.5 N/kg
a) 4 N    b) 400 N    c) 2.5 N    d) 4000 N    e) 250 N

m = W (Kongo) /gKongo = 40 kg;
W(earth) = mg = (40 kg)(10 N/kg) = 400 N

Plotted at the left is the behavior of a spring that follows Hooke’s law after an initial amount of force, F0, is applied: F = kx + F0.
4. What is the spring constant k of this spring in the region shown? (Note: the zero of each scale does not appear in the region of the graph shown)
a) 4.0 N/cm
b) 3.0 N/cm
c) 5.0 N/cm
d) 2.0 N/cm
e) 3.5 N/cm

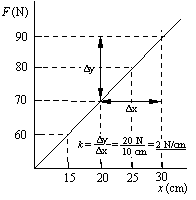
5. Assume this spring continues to behave as shown for smaller values of the stretch down to x = 0. Substitute a value for F and x at one point on the line into the equation of the line, F = kx + F0, to determine, F0, the force when the spring just begins to stretch.
a) 0 N    b) 5 N    c) 10 N    d) 20 N    e) 30 N

F0 = F – kx = 70 N – (2 N/cm)(20 cm) = 30 N

Standing on the ground is Mr. Lego, consisting of 7 body parts each a mass, m, connected by a massless skeleton, as shown on the left; four vertical bones are labeled 1 – 4.

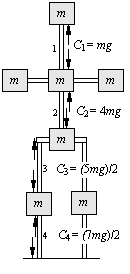
6. Draw on the figure to the left the compression vectors (arbitrary length) acting on the masses in the vertical bones #1 to #4, and label them, C1 to C4, respectively.
See picture at left.

 7. What is the magnitude of C1, the compression in bone #1?
a) 1.0 mg    b) 2.5 mg    c) 3.0 mg    d) 3.5 mg    e) 4.0 mg

 8. What is the magnitude of C2, the compression in bone #2?
a) 1.0 mg    b) 2.5 mg    c) 3.0 mg    d) 3.5 mg    e) 4.0 mg

 9. What is the magnitude of C4, the compression in bone #4?
a) 1.0 mg    b) 2.5 mg    c) 3.0 mg    d) 3.5 mg    e) 4.0 mg

10. What is the magnitude of the net gravitational force acting on earth from these masses?
a) 1.0 mg    b) 3.0 mg    c) 5.0 mg    d) 7.0 mg    e) 9.0 mg

Figure for 11-15

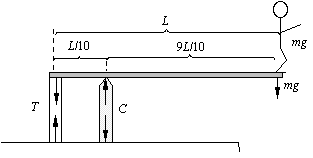
A diver (W = –mg) is at the end of a diving board L meters long. The board is tied to the ground at the rear with a post (with tension T) and rests on a point support, a pivot point (with compression C), 1/10 of the length from the left end.

11. Draw force vectors, CD (diver), C (pivot), and tension, T (rear), acting on the board.
See above picture.

12. How far is the diver from the pivot? a) 1.0 L,    b) 0.9 L,    c) 0.1 L,   d) 1.1 L,    e) 9.0 L

13. What are the torque vectors about the pivot generated by (+ is clockwise)
the diver tD = +mg(9L/10) , and at rear tR = –T(L/10)

+mg(9L/10) + [–T(L/10)] = 0
T = 9mg
T = –9mg
C + T–mg = C + (–9mg) –mg = 0
C = +10mg
14-15(two points) Determine the vector forces T and C acting on the board.
a.) T = -2mg and C = +mg
b.) T = +mg and C = -2mg
c.) T = 2mg and C = -mg
d.) T = -9mg and C = +10mg
e.) T = -10mg and C = +9mg
Back to Homework List