HW 9: Ch. 8, Problems 1-17, and Ch. 9 Problems 1-4. 1. If a force acting on you is not gravity nor a nuclear force, it is electromagnetic in nature.

2. A net force acts on a mass in the direction opposite to its motion. As the mass moves the work done on it by that force is negative.

3 A net force acts on a mass and is in the same direction as its motion. As it moves the work done on it by that force is positive.

4. When a net force does positive work on a mass it moves in the same direction as the force. A mass that moves in the oppposite direction to the net force does a negative amount of work on it.

5. The two forces acting on a mass when it is slowly raised by hand from the floor to a table by a human being are the human's force and gravity . The signs of the work done by these two forces are opposite.

6. If a mass starts at rest, moves in one direction for a while, but then returns to rest at the same place it started the net work done by the conservative forces is zero.

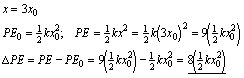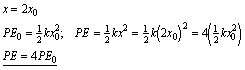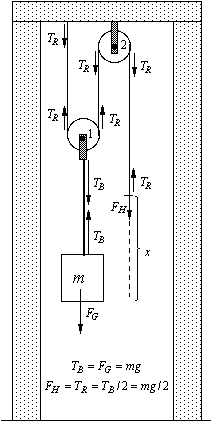
The mass in the figure (all other objects are massless) is raised when the end of the rope is slowly pulled down a distance x.

The force vectors active on the mass (use m), on the end of the rope, and within the rope and bar are shown:

7. The force that must be applied to the end of the rope to keep the mass stationary is F = mg/2.

8. If the end of the rope moves downward a distance, x, at a constant slow speed the force is: F = mg/2.

9. When the rope is pulled down the distance x, (as in 8), the work done on the rope is: (– is down)

w = F×s = (–mg/2)×(–x) = +mgx/2 .

10. The force is mg in the bar (dark line) attached to the mass during the motion (as in 8).

11a. The mass moves upward a distance x/2 when the rope is pulled down the distance, x (as in 8).

11b. The work done on the mass by the bar is:

w = F×s = (+mg)×(+x/2) = +mgx/2 .

12. The work done on the rope is equal to the work done on the mass by the bar. This is so because: The rope is connected to the bar via pulleys; the forces on the rope and mass are different due to the pulleys, but the work done by the bar on the mass is accomplished by doing the same amount of work on the end of the rope.

13. An ideal spring with spring constant, k , that is stretched a distance, x , from its normal length stores a potential energy of 1/2kx2 . If the spring is compressed by the same distance the stored potential energy is 1/2kx2. The sign of the work done on the spring by the stretching forces is  +  and by compressing forces is also  + .

14. Two springs have spring constants, k1, and k2, and are stretched by distances , x1 and x1, respectively . The ratio of the spring constants to store the same potential is :

15. If I want to store the most energy for a given stretch of the combination I connect the two identical springs in parallel :

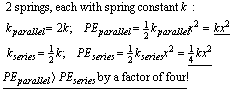
16. If I want to store the most energy for a given force applied to the combination I connect two identical springs in series :

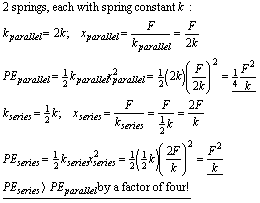
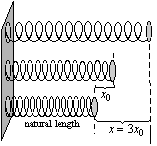
 17. A spring with spring constant, k , starts with a stretch, x = x0, and is then stretched to a further distance where,

x = 3x0. The potential energy is added (D PE) to the spring during the second stretch is: (express your answer using only k and x0)

Chapter 9 Problems 1-4

1. If the net work done on a mass as it moves is negative its kinetic energy decreases

2. When a mass is slowly raised from the floor to a table by a human being the two forces acting on the mass during the motion are the hand force and gravity. The signs of the work done by the two forces are opposite .

3. A spring that is stretched or compressed stores potential energy .

7. The potential energy stored in a spring increases by factor of 4, when the amount of stretch is doubled.

4. A mass that comes to rest by compressing a spring converts kinetic energy of the mass into potential energy stored by the spring

Back to Homework List