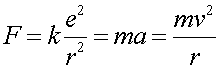Bohr's atom

Consider an electron of charge -e in a circular orbit of radius r₀ in the presence of a Coulomb force F caused by a proton of equal but opposite charge. Writing F = ma,

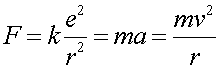    (1)

Using the fact that the momentum p = mv, and that the momentum is given in terms of the DeBroglie wavelength

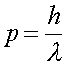    (2)

allows one to write the velocity in terms of the DeBroglie wavelength

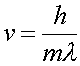    (3)

One can then write Eq. (1) with the DeBroglie wavelength rather than with the velocity.

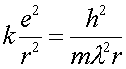    (4)

Then, Bohr made the jump that the wave function closed in on itself and that the circumference of the orbit was an integral number of wavelengths.

    (5)

Combining Eq.s (4) and (5) allows one to eliminate the wavelength and solve for the radius.

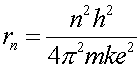    (6)

This actually perfectly agrees with the result from Schroedinger's equation, which is the more correct way to solve the problem. The accidental agreementof this proof is only true for 1/r potentials.