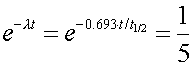
Examples for radioactivity
Example #1
Problem:
One mole of radioactive atoms has a half life of 100 years. After 7500 years, what is the number of atoms that remain?
Solution:
First find the decay constant, l, in inverse years using l = 0.693/t1/2. Then the number left is Avogadro's number times exp(-l*7500)
16
Example #2
Problem:
One measures 50,000 decays of a radioactive sample in 20 seconds. One measures the same sample 50 days later and observes only 10,000 decays in 20 seconds. What is the half life of the radioactivity.
Solution:
Since the number of decays in a given time interval are proportional to the number of undecayed nuclei, one knows that one fifth of the original nuclei still exist after 50 days. One can then state
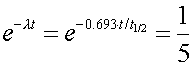
where the time t is 50 days. One can then solve for the half life by taking the natural logarithm of both sides of the equation.
t1/2 = 21.5 days
Example #3
Problem:
A beam of 8.0 MeV protons is aimed at a rat whose mass is 2.0 kg. If the RBE of the radiation is 10 and the biologically equivalent dose absorbed by the rat is 250 rems, how many protons did the rat absorb?
Solution:
The dose is: 250 rems = (Energy of a proton in Joules / 0.01) *(number of protons)*RBE/(mass of rat). After converting the energy of 8 MeV into Joules, one can solve the above equation for the number of protons.
N = 3.9 E11