


Next: Sample problem: Damped harmonic
Up: SUMMARY OF THE PHYSICS
Previous: Sample problem: Diffraction Gratings
The basic laws of circuits containing inductors (inductance L in
Henries, H), resistors (resistance R in Ohms, 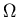 )
and
capacitors (capacitance C in Farads, F) relate the current i
in these elements to the voltage V across them,
)
and
capacitors (capacitance C in Farads, F) relate the current i
in these elements to the voltage V across them,
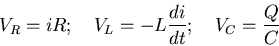 |
(4) |
where the charge
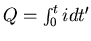 is the integral of the
current. If these three elements are combined in series in a ciruit, and are
also driven by an alternating voltage source
is the integral of the
current. If these three elements are combined in series in a ciruit, and are
also driven by an alternating voltage source
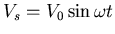 ,
then the equation for the current in the circuit as a function of time is:
,
then the equation for the current in the circuit as a function of time is:
Taking a derivative of this equation leads to the damped harmonic oscillator
equation,
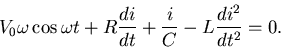 |
(6) |
The damped harmonic oscillator equation also applies to damped pendulums and
to damped mass-spring systems. In these problems is is important to
distinguish between transients and steady state response. If there is
no driving term then the behavior is only transient and is classified
as underdamped or overdamped. If there is no damping then there
is a natural frequency
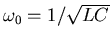 .
When the system is
``driven'' and the damping is not too large there is a special drive
frequency (e.g.
.
When the system is
``driven'' and the damping is not too large there is a special drive
frequency (e.g.
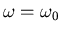 for no damping) at which the amplitude
of the response gets large. This is the phenomenon of resonance. In
the driven case there are also transients but they are rather complex and
are not treated in most undergraduate courses.
for no damping) at which the amplitude
of the response gets large. This is the phenomenon of resonance. In
the driven case there are also transients but they are rather complex and
are not treated in most undergraduate courses.



Next: Sample problem: Damped harmonic
Up: SUMMARY OF THE PHYSICS
Previous: Sample problem: Diffraction Gratings
Aleksandar Donev
1999-12-06