


Next: Sample problem: Perpendicular magnetic
Up: SUMMARY OF THE PHYSICS
Previous: Sample problem: Current loop
Once we have found electric and magnetic fields, we can control the motion
of charged particles using them. This is how a TV, a mass spectrometer, a
cyclotron and and many other devices work. The key equation is the Lorentz
force law:
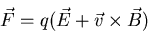 |
(3) |
This gives the force on a particle of charge q moving at velocity 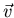 and being acted upon by an electric field
and being acted upon by an electric field 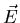 and a magnetic field
and a magnetic field 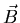 .
To find the motion of the particle, just use Newton's law
.
To find the motion of the particle, just use Newton's law
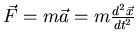 ,
where
,
where 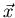 is the position of
the particle. Qualitatively, the charge is accelerated along the direction
of the electric field, while it ``spirals'' around the direction of the
magnetic field. Very complex motion can occur when these two basic motions
are combined, especially if the electric and magnetic fields change in space
and time.
is the position of
the particle. Qualitatively, the charge is accelerated along the direction
of the electric field, while it ``spirals'' around the direction of the
magnetic field. Very complex motion can occur when these two basic motions
are combined, especially if the electric and magnetic fields change in space
and time.
Aleksandar Donev
1999-12-06