Quantum Physics I PHY471, Fall 1999

Homework set 3

Due Monday, 9/20/1999

Please clearly state your assumptions, number the equations and indicate logical connections between different lines.

1. [2+2 pt] Fourier transform III

a) Find the Fourier transform of the Dirac Delta “function”.

b) Find the Fourier transform of the function f(x) = C, where C is a constant for all values of x.

2. [1+1+1+1+3+3pt] Wave packets

Consider a wave packet of the form

a) What is the dispersion relation for this wave packet?

b) What is the phase velocity of this wave packet?

c) What is the group velocity for this wave packet?

d) What is the classical velocity of the particle? Compare to the group and phase velocities.

e) Now assume that the dispersion relation is a general function Expand this function around k₀ in a Taylor series and ignore term of second order and higher. Show that the group velocity is , i.e. that the probability of the wave packet can be written as .

f) For a relativistic particle with , find the group velocity and compare with the particle velocity.

3. [4+2 pt] Gaussian wavepacket

Show how equation (74) in Ohanian chapter 2 follows from equation (73) in Ohanian chapter 2.

a) Use an expression for from your integral table and show that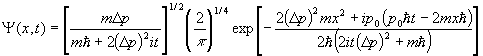

b) Now evaluate .