Quantum Physics I PHY471, Fall 1999

Homework set 8

Due Monday, 11/01/1999

1. [3 pt] Ohanian #15, p. 94

2. [1+1+2+2+2+2] Unbound states of the finite square well

Consider the unbound states (E>0) of the finite square well 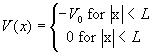. For a wave incident from the left, the solution to the Schrödinger equation can be written as .

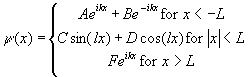a) Determine k and l.

b) Write down equations for all four boundary conditions for this problem.

c) Use the boundary conditions at x=+L to express C in terms of F and to express D in terms of F.

d) Use your results from c) and the boundary conditions at x=-L to eliminate A and to show that B can be expressed in terms of F as with .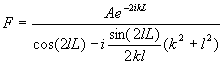

e) Plot the transmission coefficient 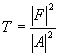versus energy over a suitable range.

f) For which values of the energy is the transmission coefficient equal to 1?

3. [1+2+2+1+1] Unbound states of the square potential barrier

Consider a particle with mass m and energy E>V₀ incident from the left on a potential .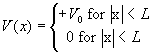

a) Write down the solution of Schrödinger’s equation for each region.

b) State the boundary conditions that apply and obtain a sufficient number of equations to determine all unknown constants.

c) Solve for the transmission coefficient and plot it versus energy over a suitable range.

d) For which values of the energy is the transmission coefficient equal to 1?

e) Which value does the transmission coefficient approach for E>>V₀?