Suggested Reading
Chapters 1, 2, 3, 4 and 5 in your text. You may defer reading 3.10, 3.11, 5.5 and 5.6.Goals
- To perform simple measurements as accurately as possible and to estimate uncertainties in these measurements.
- To gain practice in computing propagation of errors.
- To investigate the distribution of random errors.
Theoretical introduction
The main purpose of this experiment is to introduce you to methods of dealing with the uncertainties of the experiment (for more background, click here). The basic procedures to correctly estimate the uncertainty in the knowledge of the measured value (the error of the measurement) include:- Estimation of the uncertainty in the values directly measured by, or read from, the measurement device (directly measured quantities, Taylor, Chapter 1);
- correct treatment of the random errors of the experiment (Chapters 4 and 5);
- calculation of the errors of the quantities which are not measured directly (the propagation of errors, Chapter 3);
- rounding off the insignificant digits in the directly measured and calculated quantities (Chapter 2 and the Appendix to this lab).
Preliminary discussion (15-30 minutes).
Before the lab, you are asked to read and understand the theoretical material for this lab (Exp1 and Taylor). Before the experiment starts, your group needs to decide which information will be relevant to your experiment. Discuss what you will do in the lab and what preliminary knowledge is required for successful completion of each step.Think about organizing your work in an efficient way. How should you use Kgraph to expedite your calculations and unit conversions (when necessary)?
Questions for the preliminary discussion.
1. Suppose during each of several measurements we find a value which lies in the same interval of the scale of the measuring device. For example, each time we measure the length to be between 176 and 177 mm, with the length between the ticks on the ruler equal to 1 mm. How do we estimate an uncertainty in our the measured length in this case?2. Now suppose we use a much more precise device (say the laser micrometer). Due to a higher precision, this device can resolve the miniscule changes in the length due to the random mechanical deformations of the object, and in each measurement we will see the slight unsystematic changes in the observed length. From these data, how can we find the most likely value of the length? How can we estimate the spread in the measurements? Which formulas will we use?
3. Next, we are going to find out if the two independent measurements from 1 and 2 are consistent with each other. Which procedure will we use? Is there a quantitative method to find out if two measured lengths are in agreement? Is there a quantitative method to estimate how certain our conclusion about the agreement or the disagreement of these measured values is?
4. If we are going to use the results of our measurements to calculate some other quantities (e.g., calculate the density of the rod using the measurements of its dimensions and the mass), which formulas will we use to calculate the mean values and the uncertainties of these quantities?
5. In our calculation, the calculator (computer) will typically return the results with as many digits is possible. However, some of these digits will be produced from the part of the input number which we do not know, and, correspondingly, they will have no real meaning. Which procedure will you follow to systematically get rid of these insignificant digits?
Density Measurements
Introduction
Your text (Sec. 1.3, p. 5) describes how Archimedes was able to determine the composition of a king's crown by measuring its density. We will attempt to perform a similar exercise, but we shall use copper instead of gold. Copper has a density of 8.94 g/cm3 at 20 degrees Celsius (C). We will consider later what to do if the temperature is not exactly 20 degrees C. Your task today is to measure the density, calculate the appropriate uncertainties and decide whether your measurement agrees with the given value.Part A
In our lab, we will use rulers, vernier calipers and micrometers. Discuss in your group the following questions:a) Which of these instruments is the most precise; the least precise? How do you know? In particular, is the calipers more precise than the ruler? Hint: try to understand if the moving scale on the caliper (the vernier) can be used to increase the precision of the length measurement compared to a simple ruler.
b) Write down the uncertainties of the length measurements with each of these instruments.
Use the ruler to measure the three dimensions of the block. Repeat these measurements with the vernier caliper and the micrometer. Assign uncertainties to your measurements. For each instrument, measure the length with the highest precision possible.
Measure the mass of your block and estimate its uncertainty.
For the ruler measurement, compute the volume of the block and its uncertainty. Make two estimates of your uncertainty using alternatively Eqs. 3.18 and 3.19 on p. 61 of the text. Which estimate is more appropriate for this calculation? Why?
Pay attention to the units. In the calculation, follow the rules for rounding off the insignificant figures. If the calculation is done correctly, the smallest significant figure in the final mean value will be of the same order as the final uncertainty.
Compute the density and its uncertainty. Use Eq. 3.18 on p. 61 of Taylor.
Calculate the density and its uncertainty using the data obtained with the help of the caliper and micrometer.
Part B
Answer the following questions:- Is your value consistent with the density of pure copper? Could it, instead, be a copper alloy? (Copper alloys (e.g. bronze and brass) have densities which can range from 7.5 g/cm3 to 10 g/cm3.). For more information, click on Alloy Densities . Try to figure out how to justify your conclusion quantitatively. (Hint: compare the discrepancy between the theoretical and experimental values with some other number).
- In the computation of density, what were the greatest sources of uncertainty? Which were the smallest?
- If you had made only one set of measurements with a ruler, would you arrive to the same answer for the Question 1? Why?
- What systematic errors might we be overlooking? Are any of these big enough to affect your estimate of uncertainty? Consider, for instance, the temperature dependence of the density of metal, irregularities in the shape of the block, and any other errors you can think of.
Useful Information
If a metal is heated, its length increases by an amountPart C
Use the density measurement to determine the material of 3 other unknown objects. Again, present the numeric arguments supporting your conclusions.In your report, include 3 measured densities of the rectangular block and the densities of 3 unknown objects, as well as the relevant uncertainties.
Random Uncertainties
In this part of the experiment we ask you to perform one of the simplest of repetitive measurements in order to investigate random and systematic errors.Part A: Time Measurements
At the front of the room is a large digital clock that is supposed to count at a constant rate of one count per second. Assume that it does count at a constant rate, but do not assume that the stated rate of one count per second is correct. The clock will count from 1 to 20, blank out for some unspecified length of time, and then begin counting again. To measure the clock's count rate, you will be given a timer whose systematic error is less than 0.001 seconds for time intervals of ten seconds or less. However, you will be relying on hand-eye coordination, which means your measurements will have random uncertainties. Your reaction time is unavoidably variable. You may also be systematically underestimating or overestimating the total time.1. Choose a counting interval at least 10 counts long and time 25 of them. One person should time while the other records the data on the data sheet belonging to the person timing. To avoid an unconscious skewing of data, the person timing should not look at the data sheet until all 25 measurements have been recorded. This is essential; otherwise, you will introduce a bias into your measuring procedure! Make a few practice runs before taking data. Also, avoid starting a timing interval on the first count. Use the first of three counts to develop a tempo with which to synchronize your start.
2. Exchange places with your partner, and time 25 more counting intervals. Thus, each person will have a data sheet with 25 timings recorded on it.
Part B: Data Analysis
1. From your data set of 25 measurements compute the average or "mean" time per count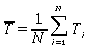 where
Ti
represent
single measurements of the time per count and N = 25, the number of measurements.
Using this value of
where
Ti
represent
single measurements of the time per count and N = 25, the number of measurements.
Using this value of 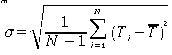
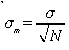
Show the calculations explicitly for the first 5 measurements but, you may use a calculator or the computers for the full 25. Read the statistics section in the Kgraph manual.
Make a bin histogram from your twenty-five measurements. The x axis should
represent the time T. It should be divided into bins, each with a width
of about
D = 0.4![]() .
The y axis should be nk, which is defined to be the number of
measurements which fall in the kth time bin. Data might fall right on the
border of two bins. Make a convention for placing these points such that
they are always placed in either the higher or the lower bin. Remain consistent
with your handling of these points.
Clearly mark the points of T
and
.
The y axis should be nk, which is defined to be the number of
measurements which fall in the kth time bin. Data might fall right on the
border of two bins. Make a convention for placing these points such that
they are always placed in either the higher or the lower bin. Remain consistent
with your handling of these points.
Clearly mark the points of T
and ![]() for your measurements. The quantity can be shown to be the best estimate
of your measurement and the region included in the
range
for your measurements. The quantity can be shown to be the best estimate
of your measurement and the region included in the
range ![]() should
contain about 68% of your data points if your errors are random and consequently
the distribution of your measurements is normal or Gaussian. With a finite
number of measurements such as 25, your distribution may not resemble the
expected "bell" shape to a great degree. The standard deviation of the
mean
should
contain about 68% of your data points if your errors are random and consequently
the distribution of your measurements is normal or Gaussian. With a finite
number of measurements such as 25, your distribution may not resemble the
expected "bell" shape to a great degree. The standard deviation of the
mean ![]() ,
is the best estimate of the uncertainty in the measurement of the mean.
Note that, unlike the standard deviation, this uncertainty can be made
arbitrarily small by taking a sufficiently large number of measurements.
,
is the best estimate of the uncertainty in the measurement of the mean.
Note that, unlike the standard deviation, this uncertainty can be made
arbitrarily small by taking a sufficiently large number of measurements.
Part C: Conclusions
1. Does a significant systematic error exist? In other words, is there a significant discrepancy in the time measured by the large clock? Note that we have already made the hypothesis that the large digital clock is running correctly, and now we want to check whether this hypothesis is in agreement with our statistical analysis.2. Using an equation similar to Eq. 5.67 on p. 150 of your text, compute the following quantity for your 25 measurements:
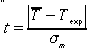
3. Assuming that your measurements follow a normal distribution, calculate
the probability P of obtaining a result
that differs from Texp
by t or more. In other words, what is the probability 1-P
that 4. Is the discrepancy
significant or not? This is somewhat a matter of opinion since we must
decide what is significant. If the probability is less than 5%, the probability
is "unreasonably" small and discrepancy is significant. On the other hand,
if the probability is greater than approximately 32%, the probability is
"rather large", and the discrepancy is not significant. In this context,
state your conclusions clearly.
5.How
many 6. Suppose you
had recorded only your first 5 measurements. What would you have concluded
about the existence of a significant discrepancy? Were the remaining 20
measurements necessary in your opinion? Explain.
1. Since
the error of the measurement is only an approximate estimate of
the uncertainty of the measurement, we do not need to keep more than one
or two largest digits in it. The smallest digit in the mean value should
be of the same order as the smallest significant digit of the uncertainty.
Examples:
2. When adding or subtracting two numbers, the result should have the same
number of the significant digits after the decimal point as the
least precise summand. Example:
![]() ?
You may need to use the table on p. 286 of your textbook, which gives the
probability P that
?
You may need to use the table on p. 286 of your textbook, which gives the
probability P that
![]() for
the Gaussian distribution with the standard
deviation
for
the Gaussian distribution with the standard
deviation ![]() ,
and
for any given t.
,
and
for any given t.
![]() is the
discrepancy
is the
discrepancy ![]() when the probability P=5%; when P=32%? From this and the previous
answer, formulate a "rule of thumb" allowing you to determine if the discrepancy
is significant or not.
when the probability P=5%; when P=32%? From this and the previous
answer, formulate a "rule of thumb" allowing you to determine if the discrepancy
is significant or not.
Structure
of the report
Appendix.
Significant figures
In
the calculations, it is always important to distinguish significant figures
in the presented numbers from insignificant. The following simple rules
will help you in this task.
Incorrect
Correct
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() or
or ![]()
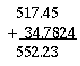
3. When multiplying or dividing, the result should have the same total number of the significant digits as the least precise multiplier. Example:
![]()
4. For other operations (raising to power, square root, exponent) the rule is similar to the one for the multiplication and division: you should keep as many significant digits in the final result as you had in the input. Example: