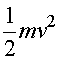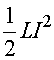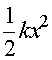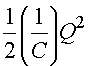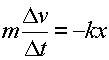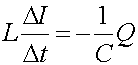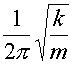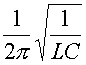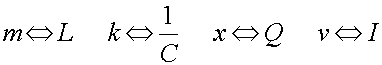LC circuits
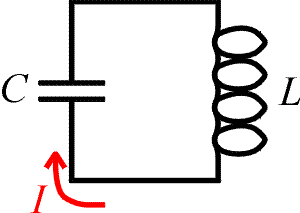 An
LC circuit is simply a closed loop with only two elements, a capacitor and an inductor. We
will show that the LC circuits have resonant properties - they respond to certain
frequencies. Therefore they can serve as the basis for any device that needs to tune to a
specific frequency such as a radio. In an LC loop the charge oscillates back and forth
through the capacitor with a given frequency just as a mass on a spring oscillates. To
demonstrate this equivalence, we list several equations for both a mechanical spring and
for an LC circuit.
An
LC circuit is simply a closed loop with only two elements, a capacitor and an inductor. We
will show that the LC circuits have resonant properties - they respond to certain
frequencies. Therefore they can serve as the basis for any device that needs to tune to a
specific frequency such as a radio. In an LC loop the charge oscillates back and forth
through the capacitor with a given frequency just as a mass on a spring oscillates. To
demonstrate this equivalence, we list several equations for both a mechanical spring and
for an LC circuit.
The parameters that determine the motion of a spring are the mass m,
spring constant k, the position x, and
the velocity v which is the rate of change of x.
The parameters that determine the behavior of an LC circuit are L,
C, Q and I
which is the rate of change of Q. Thus there is a one-to-one
correspondence since the equations of motion are identical given the substitutions:
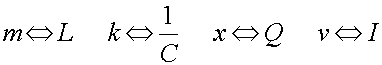
The characteristic frequency of and LC circuit is the
frequency at which large amplitudes are built up when a driving force comes in at that
frequency. A child on a swing will be sensitive to a pushing force which comes regularly
with the natural frequency of the swing. A force that comes at a different frequency will
not build up a large amplitude as it will often be pushing against the child's motion. We
call this the resonant frequency.
Examples AC circuits's index
 An
LC circuit is simply a closed loop with only two elements, a capacitor and an inductor. We
will show that the LC circuits have resonant properties - they respond to certain
frequencies. Therefore they can serve as the basis for any device that needs to tune to a
specific frequency such as a radio. In an LC loop the charge oscillates back and forth
through the capacitor with a given frequency just as a mass on a spring oscillates. To
demonstrate this equivalence, we list several equations for both a mechanical spring and
for an LC circuit.
An
LC circuit is simply a closed loop with only two elements, a capacitor and an inductor. We
will show that the LC circuits have resonant properties - they respond to certain
frequencies. Therefore they can serve as the basis for any device that needs to tune to a
specific frequency such as a radio. In an LC loop the charge oscillates back and forth
through the capacitor with a given frequency just as a mass on a spring oscillates. To
demonstrate this equivalence, we list several equations for both a mechanical spring and
for an LC circuit.