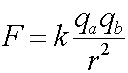where k = 8.99E9 (Nm2/C2)
, r = 2*6.37E6 (m)
, qa = qb
= NA*e , e = 1.602E-19 (C)
, and NA = Avogadro's number =
6.02E23Examples for Coulomb's law
Example #1
Problem:
How many coulomb's of charge is contained in the electrons of one kg of hydrogen?
Solution:
One kg of hydrogen is 1000 grams, and has therefore 1000 times Avagadro's number of electrons.
Q = 1000* NA * e
where e = 1.602E-19 (C) , and NA = Avogadro's number = 6.02E23
Q = -9.64E7 C
Example #2
Problem:
Consider one gram of hydrogen gas which has been separated into its electrons and protons. The electrons are placed on Earth's north pole and the protons are placed on Earth's south pole. What is the magnitude of the force the electrons feel due to the presence of the protons?
Solution:
Remember that one gram of H gas has one mole (Avagadro's number) of hydrogen atoms.
The force between the two is given by Coulomb's law:
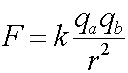where k = 8.99E9 (Nm2/C2)
, r = 2*6.37E6 (m)
, qa = qb
= NA*e , e = 1.602E-19 (C)
, and NA = Avogadro's number =
6.02E23
F = 5.14E5 (N)
Example #3
Problem:
What is the elecric force between 2 u-quarks separated by 1.0E-16 meters? This is a typical separation inside a proton.
Given: The charge of an up quark is (2/3)e.
Solution:
The force between the two is given by Coulomb's law:
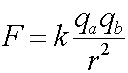where r
= 1.0E-16 (m) , qa
= qb = (2/3)*e
F = 1.03E4 (N)
Example #4
Problem:
Two charges feel a repulsive force of 96 (N). What is the force if the separation, r, is quadrupled.
Solution:
Since Coulomb's law scales as r-2, and r becomes larger by a factor of 4, the new force should be (1/4) squared, or one sixteenth of the old force.
F = 96/16 (N)
F = 6.0 (N)
Example #5
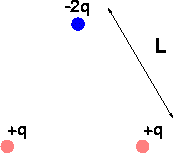
Problem A:
Imagine 3 charges, separated in an equilateral triangle as shown above, with L = 2.0 cm, q = 1.0 nC. What is the magnitude and direction of the force felt by the upper charge?
Solution:
The Force due to the lower left charge has a magnitude:
where the factor of 2 comes from the fact that the upper charge is 2q. The direction of this contribution is 30 degrees from vertical. After adding in the contribution from the lower right charge, the net force felt by a will be in the vertical direction, and downwards since it is attractive. Thus multiply the magnitude above by 2cos(30o), where the factor of 2 is from two charges and the cos(30o) projects out the vertical component. (Remember cos(30o) is sqrt(3/2)
= 7.79E-5 (N), down
Problem B:
What is the net electric potential energy of the configuration?
Solution:
The net Potential energy is the sum of three contributions. For 3 charges a,b,c it is the sum of the ab part, the ac part and the bc part. The contribution from the lower two charges is kq2/L, while the contribution of the pairs which include the upper charge is -2 time this, thus the sum is:
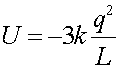
=1.35E-6 (J)
Problem C:
How much energy does it cost to remove the upper charge?
Solution:
This is just the sum of the two terms used above that include the upper charge.
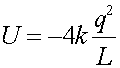
=-1.80E-6 (J)