RC Circuits
An RC circuit is simply a circuit with both a resistor and a capacitor. This combination is useful to study because capacitors can be used to store energy and a resistor placed along with the capacitor can control the rate at which energy is released from the capacitor.
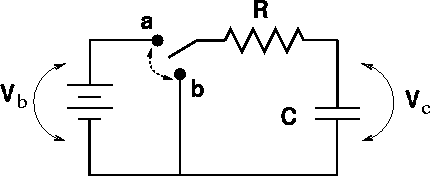
We will confine our studies to the following type of RC circuit.

A switch can be moved from position a to position b. Before we go further, let us review some facts about capacitors:
The charge across a capacitor can not change instantaneously. Since the change in charge DQ = IDt, there must always be a non-zero time before the charge can change a non-zero amount, unless there were an infinite current.
There is no current across a capacitor in steady state. Since charge builds up on capacitor instead of flowing through it, current can build up until the point that the voltage V=Q/C will balance out the external voltage pushing charge onto the capacitor.
When a capacitor of capacitance C is in series with a battery of voltage Vb and a resistor of resistance R, the voltage drops must be:
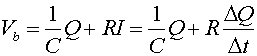 ,
,
which is a statement that the voltage gained going across the battery must equal the voltage drop across the capacitor plus the voltage drop across the resistor. An equation where the rate of change of a quantitity (DQ/Dt) is proportional to the quantity (DQ) will always have an exponential solution. We consider two instances:
Discharging the capacitor: The capacitor initially is connected (switch in position a) for a long time, and is then disconnected by moving the switch to b at time t = 0. The capacitor then discharges, leaving the capacitor without charge or voltage after a long time.
Charging the capacitor: The switch is in position b for a long time, allowing the capacitor to have no charge. At time t = 0, the switch is changed to a and the capacitor charges.
| Discharging | Charging | |
| Charge | ||
| Current | ||
| Voltage |
Here, Q0, V0 and I0 refer to the charge, voltage and current of the capacitor in the instant after the switch is thrown. The time t is the characteristic time of the decay, t = RC. When confronted with an RC problem, the best strategy is the following:
Decide what the charge across the capacitor was just before the switch was thrown. Since the charge can not change instantly, this is the charge just after the switch is thrown.
Decide what the charge is long after the switch is thrown.
Pick the exponential form for the charge Q(t) to satisfy the correct initial and final charges.
The voltage across the capacitor can be found through, V = Q/C. The voltages across the other elements can be found with the help of Kirchoff's first law.
The current through a capacitor must always decay and end up at zero, since charge can not contiuously flow through a capacitor. The initial current can usually be ascertained with the help of Ohm's law, V=RI.
The characteristic time t = RC tells one that the charging/discharging is slower with a larger resistor or capacitor. This makes sense, because a larger resistor impedes the flow of current; thus slowing the charging/discharging, and a larger capacitor holds more charge; thus requiring more time to charge.
Everyone should have a good feeling for exponential functions. Below are sketches of the charge Q(t) for the charging and discharging capacitors.
ajglkajla