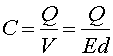
Examples for capacitors

Example #1

Problem:

Consider two plates separated by d=1.5 cm , where the electric field between them is 100 V/m, and the charge on the plates is 30.0 mC. What is the capacitance?

Solution:

The Capacitance is:

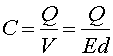
2.0E-5 F

Example #2

Problem:

Consider a capacitor made of two 0.05 m² plates separated by 0.5 mm. If the capacitance is 3.0 nf, what is the relative permeability, k, of the material between the plates?

Solution:

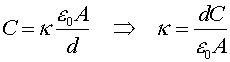
3.4

Example #3

Problem: part a.)

What is the capacitance of the following segment of a circuit?

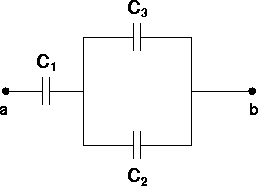
DATA: C₁=C₂=C₃=3.0 mf

Solution:

The capacitance of the two in parallel is C₂₃=C₂+C₃. The capacitance of the entire circuit is:

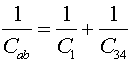
2.0 (mF)

part b.)

If a voltage V_ab = 6.0 V is applied, what is the charge on each capacitor?

Solution:

The charge on the first capacitor is the same as the charge on the whole combination, since it is the only thing the left-hand wire is connected to. This charge can be found from the capacitance.

There is a charge Q₁ on the opposite side of the first capacitor, which must have come equally from the next capacitors since they are equal to each other. Therefore, Q₂=Q₃=(1/2)Q₁.

Q₁ = 12 mC,     Q₂ = Q₃ = 6.0 mC

part c.)

What is the voltage across each capacitor?

Solution:

Use V_i=Q_i/C_i. Check when you are done that the voltages add up to 6.0 V.

V₁ = 4.0 V,     V₂ = V₃ = 2.0 V

Example #4

Problem:

A capacitor has a charge of 3.0 nC when the voltage across the capacitor is 12 V. What is the energy stored in the capacitor?

Solution:

The energy is:

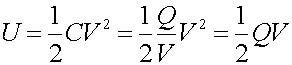
18 E-9 J

Capacitors index        Lecture index