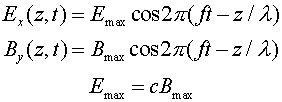Maxwell's equations and light
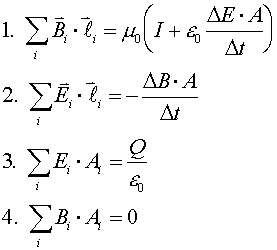 Light is an electromagnetic wave. Radio signals and X-rays are also electromagnetic waves.
They can be understood using Maxwell's equations, the four equations that govern all of
electricity and magnetism. The first equation is Ampere's law, which in its complete form includes
a term on its right-hand side that we have not discussed before.
The second equation is Lenz's law. The third equation is Gauss's law, which expresses the fact
that electric field lines begin and end only at charges. The fourth equation is the
magnetic equivalent of Gauss's law, which expresses the fact that magnetic field lines never
begin or end.
Light is an electromagnetic wave. Radio signals and X-rays are also electromagnetic waves.
They can be understood using Maxwell's equations, the four equations that govern all of
electricity and magnetism. The first equation is Ampere's law, which in its complete form includes
a term on its right-hand side that we have not discussed before.
The second equation is Lenz's law. The third equation is Gauss's law, which expresses the fact
that electric field lines begin and end only at charges. The fourth equation is the
magnetic equivalent of Gauss's law, which expresses the fact that magnetic field lines never
begin or end.
After a bit of non-trivial differential
calculus one can show that both the electric and magnetic field obey wave equations. The
speed c of an electromagnetic wave is given by: c
=1/(e0m0)1/2 =
2.998 X 108m/s.
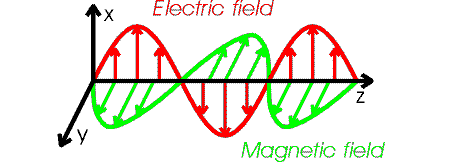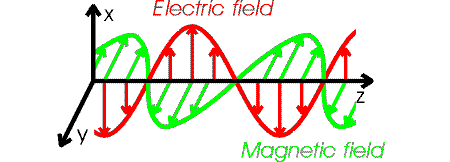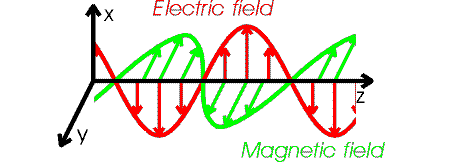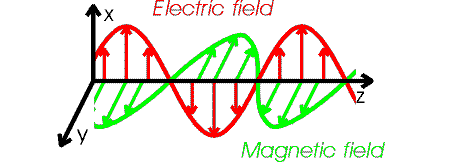
The details of an electromagnetic wave are
fairly complicated. The electric and magnetic field vectors point in directions that
are perpendicular to each other, and perpendicular to the direction the wave is travelling.
If the wave moves in z-direction, and the
electric field oscillates in the x-direction, then the
magnetic field oscillates in the y-direction.
Such a wave is said to be polarized in the x-direction.
(Polarization is described in terms of the electric field rather than the magnetic field because
the electric field more easily interacts with materials.)
The figure below illustrates the behavior of an electromagnetic wave which is polarized
along the x-axis.
The forms of the electric and magnetic field
in the wave are:
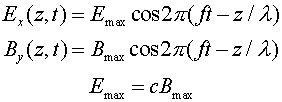
where the frequency and wavelength are related by c
= fl.
Electromagnetic
waves index
examples
Lecture index
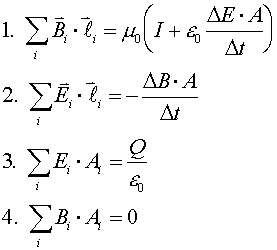 Light is an electromagnetic wave. Radio signals and X-rays are also electromagnetic waves.
They can be understood using Maxwell's equations, the four equations that govern all of
electricity and magnetism. The first equation is Ampere's law, which in its complete form includes
a term on its right-hand side that we have not discussed before.
The second equation is Lenz's law. The third equation is Gauss's law, which expresses the fact
that electric field lines begin and end only at charges. The fourth equation is the
magnetic equivalent of Gauss's law, which expresses the fact that magnetic field lines never
begin or end.
Light is an electromagnetic wave. Radio signals and X-rays are also electromagnetic waves.
They can be understood using Maxwell's equations, the four equations that govern all of
electricity and magnetism. The first equation is Ampere's law, which in its complete form includes
a term on its right-hand side that we have not discussed before.
The second equation is Lenz's law. The third equation is Gauss's law, which expresses the fact
that electric field lines begin and end only at charges. The fourth equation is the
magnetic equivalent of Gauss's law, which expresses the fact that magnetic field lines never
begin or end.