Electric fields for simple geometries

Gauss's law can be used to derive the E-field for the following geometries:

1. Spherically symmetric charge distributions .
   Choose the Gaussian surface to be a sphere. The area of the surface is 4p r², so Gauss's law says 4p r² E = 4p k Q. That implies E = k Q / r² where Q is the charge inside the chosen radius r.

   For a point charge, this just gives good old Coulomb's law.

   For a charge Q uniformly distributed over the surface of a sphere of radius R, it says that the field inside that sphere (r < R) is zero, and the field outside it is just like that due to a point charge at its center. (Possibly you recall learning a similar result for gravity last semester.)

2. A large plate with uniform charge density.
   Consider the plate below, which we will assume is infinite (a good assumption if you are close to the plate) and has a charge per unit area, s.        
                
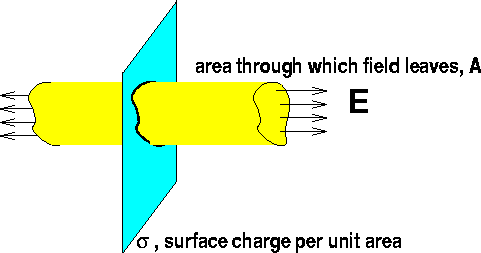
   Gauss's law states (remember the field leaves through both sides):
   

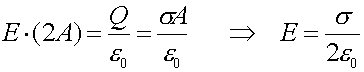3. Two oppositely charged parallel plates.
   If you have two plates with opposite charge, as in the parallel plate capacitor, the electric fields would add together to give twice this value in between the plates, 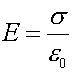,and zero outside. The field between the plates can also be written as E = 4 pi k q / a, where q is the charge on one plate, and a is the area of one plate.

4. An infinite line charge. (Not discussed this year)
   Drawing a cylinder of length L around an infinite wire, which has a charge per unit length of l, will trap a charge inside of Q=lL, and the area through which the flux leaves is 2prL. Gauss's law then states:
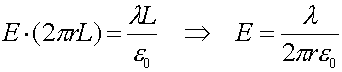