When to use Kirchhoff's laws

Here are three typical circuit diagrams which might need to be solved (e.g. given the resistances of all the resistors and the voltages of all the batteries, find all of the currents).

The figure on the left can be solved easily using the rules for adding resistances in parallel and series. Resistors R₃, R₄ and R₅ can be treated as if they were a single resistor of resistance R₃₄₅. This effective resistance can be added in parallel with R₂ to give another effective resistance R₂₃₄₅. Finally, that effective resistance can be added in series with R₁ to calculate the net resistance R = R₁ + R₂₃₄₅ seen by the battery. This value of R can be used to compute the current produced by the battery. The current from the battery all flows through R₁, so the voltage drop across R₁ can be computed using Ohm's law. Since the battery voltage is known, you can next compute the voltage drop across R₂. Now applying Ohm's law to R₂ tells you the current through it; etc. In this way you eventually figure out the currents and voltage drops everywhere in the circuit.

The middle and right-side figures cannot be solved by such a (simple?) strategy. Instead, you have to write down Kirchhoff's laws and solve the equations.

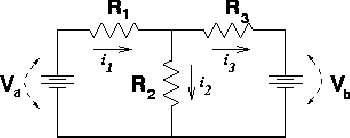
For instance consider the right-hand figure. Give names to the unknown currents i1, i2 and i3 through the 3 resistors (choosing the directions ad lib). These unknown currents can be found by solving 3 equations:

1. The first equation describes current conservation into the the node.
2. The second equation expresses the requirement that voltage losses cancel voltage gains for the loop on the left.

3. The third equation expresses the same for the loop on the right. Note that if one makes a counter-clockwise loop, one goes against the current through R₃ and the sign of that term is therefore opposite the normal one.