Eye glasses and contact lenses
The human eye has a lens that forms a real image on the back of the eye, where receptors (rods for dim light; cones for high resolution and color) detect the light and relay signals to the brain. (The signals sent to the brain are not actually just what the receptors detect -- there is considerable "processing" before the optic nerve.) By flexing part of the lens, you can change the focal length f of your eye to focus objects that are located anywhere between your near point and your far point for that eye.
The near point is defined as the closest point at which an object can still be brought into focus. Similarly the far point is the defined as the farthest point that can be brought into focus. The normal near point is defined as 25cm, while the normal far point is at infinity. These "normal" values are defined by the range that is considered adequate for standard functioning in our visual world. Many eyes, especially young ones, can focus closer than 25 cm, and can also focus "beyond" infinity (i.e., they can focus rays that have passed through a converging lens that makes them slightly converging when they reach the eye.) Many eyes, especially older ones, have a near point larger than 25cm, and/or a far point that is smaller than infinity
If an individual's near point is beyond the normal near point, the person is called far-sighted (hyperopic), since the person can focus only on far-away objects. If an individual's far point is closer than infinity, that person is near-sighted (myopic). It is possible to be both near-sighted and far-sighted in the same eye, as frequently happens in older people due to a decline in the range of variation of f with age.
Corrective lenses are converging (convex) for far-sightedness, or diverging (concave) for near-sightedness; or both (one above the other in the form of bifocals) for an eye that needs correction at both short and long distances. The corrective lens for near-sightedness creates an image at the person's actual near point for an object at the desired "normal" near point of 25cm. The corrective lens for far-sightedness creates an image at the person's actual far point for an object that is at infinity. In either case, the image is on the same side of the lens as the object. Hence the image is virtual and not inverted. The magnification is somewhat different from 1.00, which can make it difficult to get used to wearing glasses, as I can report first hand.
Physicists usually specify lenses by their focal lengths. But especially in the eyeglass business, it is traditional to specify the strength of a lens in terms of the refractive power, which is measured in diopters, and which is defined as the inverse of the focal length, with the focal length measured in meters. Lenses with shorter focal lengths are stronger lenses, and have larger refractive power.
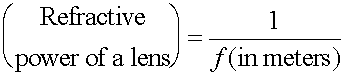
The refractive power of a lens, just like the focal length, is positive for a converging (convex) lens and negative for a diverging (concave) lens. On the next two pages, the procedure for calculating a lens prescription will be demonstrated for the near- and far-sighted cases. (In real life, there is a little more to lens prescriptions than this. For example, the lens of an eye is often not symmetric, e.g., its focal length in the vertical plane may be different from its focal length in the horizontal plane.)