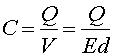
Examples for capacitors
Example #1
Problem:
Consider two plates separated by d=1.5 cm , where the electric field between them is 100 V/m, and the charge on the plates is 30.0 mC. What is the capacitance?
Solution:
The Capacitance is:
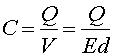
2.0E-5 F
Example #2
Problem:
Consider a capacitor made of two 0.05 m2 plates separated by 0.5 mm. If the capacitance is 3.0 nf, what is the relative permeability, k, of the material between the plates?
Solution:
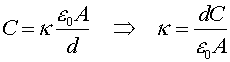
3.4
Example #3
Problem: part a.)
What is the capacitance of the following segment of a circuit?
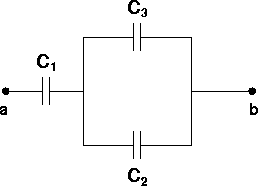
DATA: C1=C2=C3=3.0 mf
Solution:
The capacitance of the two in parallel is C23=C2+C3. The capacitance of the entire circuit is:
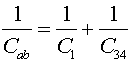
2.0 (mF)
part b.)
If a voltage Vab = 6.0 V is applied, what is the charge on each capacitor?
Solution:
The charge on the first capacitor is the same as the charge on the whole combination, since it is the only thing the left-hand wire is connected to. This charge can be found from the capacitance.
![]()
There is a charge Q1 on the opposite side of the first capacitor, which must have come equally from the next capacitors since they are equal to each other. Therefore, Q2=Q3=(1/2)Q1.
Q1 = 12 mC, Q2 = Q3 = 6.0 mC
part c.)
What is the voltage across each capacitor?
Solution:
Use Vi=Qi/Ci. Check when you are done that the voltages add up to 6.0 V.
V1 = 4.0 V, V2 = V3 = 2.0 V
Example #4
Problem:
A capacitor has a charge of 3.0 nC when the voltage across the capacitor is 12 V. What is the energy stored in the capacitor?
Solution:
The energy is:
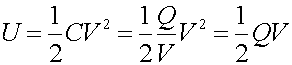
18 E-9 J