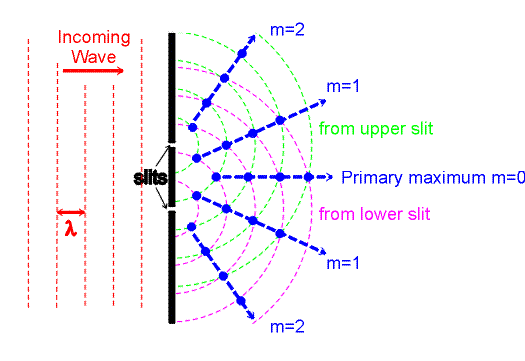
Two-slit interference
The prototypical example of interference is the two-slit experiment. Consider monochromatic (single wavelength) light incident on two narrow slits as shown.

Wave crests leaving the upper and lower slits at a given instant of time are indicated by the violet and green lines. In the directions shown by the blue lines, the violet and green waves rise and fall together, giving constructive interference in those directions. Midway between those directions, the two contributions are 180 degrees out of phase, so they tend to cancel one another. The result is that if a screen is placed to the right, an interference pattern is seen: there are peaks in the brightness in the direction of the blue arrows, with dark bands in between.
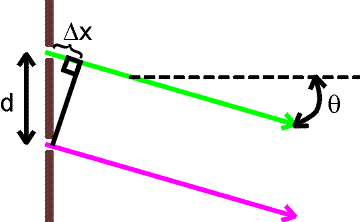 To solve for the angular position of the maxima, consider two rays emited at an angle
q from each of the slits.
The screen is assumed to be very far away (in comparison to the distance between the slits),
so the rays from to the two slits to any given point on the screen are nearly parallel.
If the distance
Dx
is an integer number m of wavelengths, a bright maximum
will appear on the screen. The formula for the positions of those maxima is
To solve for the angular position of the maxima, consider two rays emited at an angle
q from each of the slits.
The screen is assumed to be very far away (in comparison to the distance between the slits),
so the rays from to the two slits to any given point on the screen are nearly parallel.
If the distance
Dx
is an integer number m of wavelengths, a bright maximum
will appear on the screen. The formula for the positions of those maxima is
![]()
where m = 0,1,2,3,...
A second formula is needed to relate the positions on the screen to the angle q. The screen, the center line, and the line to an arbitrary point on the screen form a right triangle, leading to the formula
tan q = y / L
where L is the distance from the slits to the screen and y is the distance measured on the screen from the forward direction (the central maximum). For two-slit interference, the interference pattern is only easy to see at rather small angles, for which it is an excellent approximation to take tan q and sin q to be equal. For diffraction gratings, however, that approximation is not necessarily adequate because pattern can be observed also at large angles.
How bright are the maxima you may ask? -- Equal contributions from each of two slits makes the E and B fields twice as large as they would have been with only one slit open. The light intensity (measured in W/m^2) is proportional to E2 and B2, so the maxima have an intensity that is 4 times greater than would be present if only 1 slit were open.