
When to use Kirchhoff's laws
Here are three typical circuit diagrams that might need to be solved (e.g. given the resistances of all the resistors and the voltages of all the batteries, find all of the currents).

The figure on the left can be solved easily using the rules for adding resistances in parallel and series. Resistors R3, R4 and R5 can be treated as if they were a single resistor of resistance R345. This effective resistance can be added in parallel with R2 to give another effective resistance R2345. Finally, that effective resistance can be added in series with R1 to calculate the net resistance R = R1 + R2345 seen by the battery. This value of R can be used to compute the current produced by the battery. The current from the battery all flows through R1, so the voltage drop across R1 can be computed using Ohm's law. Since the battery voltage is known, you can next compute the voltage drop across R2. Now applying Ohm's law to R2 tells you the current through it; etc. In this way you eventually figure out the currents and voltage drops everywhere in the circuit.
The middle and right-side figures cannot be solved by such a simple(?) strategy. Instead, you must write down Kirchhoff's laws and solve the equations.
| For
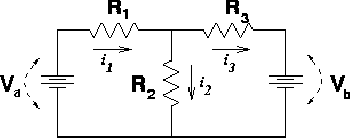
instance consider the right-hand figure. Give names to the
unknown currents
i1,
i2
and i3
through the 3 resistors (choosing the directions ad lib).
These unknown currents can be found by solving 3
equations: |
|
You could also write an equation for a third loop that is defined by traveling around the outside of the circuit. That equation would be slightly more complicated because it would involve both batteries; but it is unnecessary since it would be merely a linear combination of Eq. 2 and Eq. 3 above.