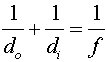 , one can solve for do.
, one can solve for do.Examples for lenses
Example #1
Problem:
a.) A converging lens (convex) has a focal length of 14 cm. Looking through the lens, one sees an image 20 cm behind the lens. Where is the object?
Solution: Since the image is behind the lens, it is virtual
and the distance di is negative. Using the formula, 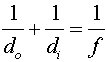 , one can solve for do.
, one can solve for do.
do = 8.24 cm
b.) If the height of the object is 1.5 cm, what is the height of the image.
Solution: Using the formula, 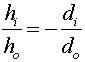 to get
to get
hi = 3.64 cm, upright
Example #2
Problem:
A real image of a coin is observed 34 cm beyond a lens. The image height is 1.4 cm and it is known that the actual coin is 0.7 cm high. What is the focal length of the lens?
Solution: First, find the object distance using 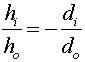 . Remember that since the image is real, that the image
height is negative. ( do =
17 cm ). One can then use
. Remember that since the image is real, that the image
height is negative. ( do =
17 cm ). One can then use 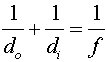 to find the focal length.
to find the focal length.
f = 11.33 cm
Example #3
Problem:
An object is place half way between a converging lens and it's focal point. The focal distance is 8 cm.
a.) Where is the image?
Solution: Use 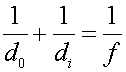 with 4
cm for do.
with 4
cm for do.
di = -8 cm
b.) What is the magnification?
m = 2