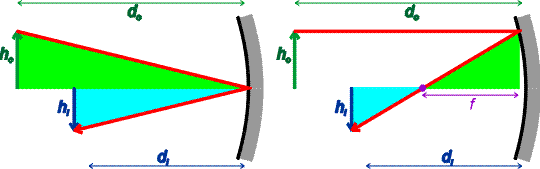
Real images
On the previous page, we assumed that the light rays approaching the mirror were all parallel. That is true for light from a distant object, but not for light from an object that is only a finite distance away from the mirror. We now derive the point at which the light is collected, the image distance, as a function of the distance the object is separated from the mirror, the object distance. Consider an object of height ho and an image of height hi below. The two triangles on the left and right are similar since they have the same angles. The two triangles on the right are also similar.

The similarity of the green and aqua triangles allows one to write
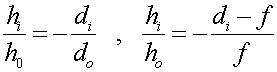
One can combine these two equations, eliminating the ratio of the object and image heights, to obtain a relationship between the distances and focal length.
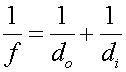
This is a remarkably useful formula. We have derived it for a concave mirror; but it will also apply to convex mirrors as well as to lenses.