PHY471 Fall 2000 Quantum Physics I

Homework set 2 Due date: Monday, 9/13/2000

1. [2pt] Series expansion

Ohanian writes on page 28 that the “factor equals zero if n ≠ m, and it equals 1 if n=m.” State the assumptions under which this is true and then prove Ohanian’s statement.

2. [1pt+2pt+2pt+3pt] Dirac Delta “function”

Prove the following identities:

(i) d(-x) = d(x)

(ii) x d(x-a) = a d(x-a)

(iii) d(cx) = d(x)/|c| for c ≠ 0

(iv)

3. [5pt] Fourier series

Consider the function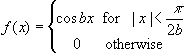
In the interval -p/(2b) < x < p/(2b)) represent the function f as a fourier series and evaluate the coefficients. Plot the fourier series of order n=1, n=2, n=3 (i.e. truncate the summation after the first, second and third terms, respectively).

4. [5pt] Fourier transform

Find the fourier transform of the same function f(x) considered in problem 3 and plot the fourier transform. Show explicitly that