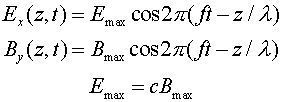Maxwell's equations and light
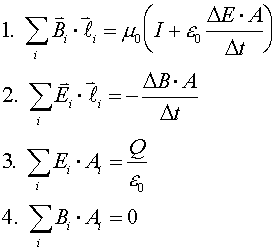 We have completed our study of the laws of electricity and magnetism. All that we have learned
can be summarized in the equations known as Maxwell's Equations, together with the formulas
for the electric and magnetic forces on a charge. One of several ways Maxwell's equations can be
written is shown at the right, just so you can say you have seen them.
The first equation is Ampere's law, (including a term on the right-hand side that we have not discussed
in this course).
The second equation is Faraday's Law combined with Lenz's law.
The third equation is Gauss's law, which expresses the fact that electric field lines begin and end
only at charges.
The fourth equation is the magnetic equivalent of Gauss's law, which expresses the fact that magnetic
field lines never begin or end (i.e., there are no free magnetic charges).
We have completed our study of the laws of electricity and magnetism. All that we have learned
can be summarized in the equations known as Maxwell's Equations, together with the formulas
for the electric and magnetic forces on a charge. One of several ways Maxwell's equations can be
written is shown at the right, just so you can say you have seen them.
The first equation is Ampere's law, (including a term on the right-hand side that we have not discussed
in this course).
The second equation is Faraday's Law combined with Lenz's law.
The third equation is Gauss's law, which expresses the fact that electric field lines begin and end
only at charges.
The fourth equation is the magnetic equivalent of Gauss's law, which expresses the fact that magnetic
field lines never begin or end (i.e., there are no free magnetic charges).
Using some not-so-simple calculus, Maxwell's equations can be
used to show that the electric and magnetic fields obey wave equations. The
speed c of an electromagnetic wave is determined by the constants of
electricity and magnetism that you know so well:
c = 1/(e0m0)1/2 =
2.998 X 108m/s.
Light is an electromagnetic wave: this was realized by Maxwell circa 1864, as soon as the equation
c = 1/(e0m0)1/2 =
2.998 X 108m/s
was discovered, since the speed of light had been accurately measured by then, and its agreement
with c was not likely to be a coincidence.
Radio signals are also electromagnetic waves; after the discovery of Maxwell's equations, it took
well less than a century to figure out how to produce and detect them to an extent that has
revolutionized our technological civilization.
Infrared light, ultraviolet light, X-rays, and gamma rays are also examples of electromagnetic waves;
like radio waves, they were unknown at the time Maxwell's equations were discovered.
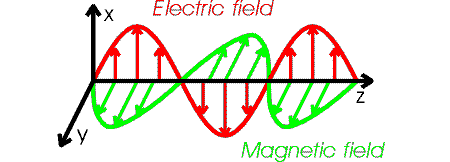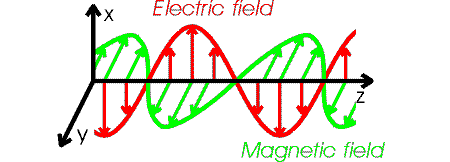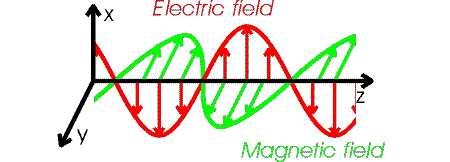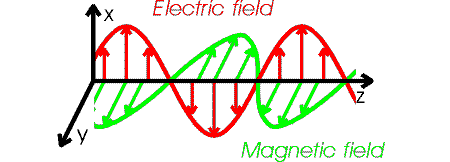
The details of an electromagnetic wave are
fairly complicated. The electric and magnetic field vectors point in directions that
are perpendicular to each other, and perpendicular to the direction the wave is travelling.
If the wave moves in z-direction, and the
electric field oscillates in the x-direction, then the
magnetic field oscillates in the y-direction.
Such a wave is said to be polarized in the x-direction.
(Polarization is described in terms of the electric field rather than the magnetic field because
the electric field interacts more readily with most materials.)
The figure below illustrates the behavior of an electromagnetic wave that is polarized
along the x-axis and travelling in the
z-direction.
The formulas for the electric and magnetic fields
in this wave are:
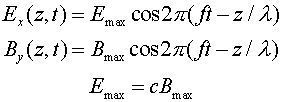
where the frequency and wavelength are related by c
= f l.
Electromagnetic
waves index
examples
Lecture index
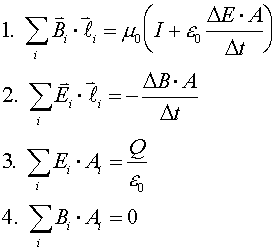 We have completed our study of the laws of electricity and magnetism. All that we have learned
can be summarized in the equations known as Maxwell's Equations, together with the formulas
for the electric and magnetic forces on a charge. One of several ways Maxwell's equations can be
written is shown at the right, just so you can say you have seen them.
The first equation is Ampere's law, (including a term on the right-hand side that we have not discussed
in this course).
The second equation is Faraday's Law combined with Lenz's law.
The third equation is Gauss's law, which expresses the fact that electric field lines begin and end
only at charges.
The fourth equation is the magnetic equivalent of Gauss's law, which expresses the fact that magnetic
field lines never begin or end (i.e., there are no free magnetic charges).
We have completed our study of the laws of electricity and magnetism. All that we have learned
can be summarized in the equations known as Maxwell's Equations, together with the formulas
for the electric and magnetic forces on a charge. One of several ways Maxwell's equations can be
written is shown at the right, just so you can say you have seen them.
The first equation is Ampere's law, (including a term on the right-hand side that we have not discussed
in this course).
The second equation is Faraday's Law combined with Lenz's law.
The third equation is Gauss's law, which expresses the fact that electric field lines begin and end
only at charges.
The fourth equation is the magnetic equivalent of Gauss's law, which expresses the fact that magnetic
field lines never begin or end (i.e., there are no free magnetic charges).