The resolving power of a lens
A circular opening is similar to the single slit just discussed, except that it exists in two dimensions instead of one. It causes its own form of diffraction pattern. In optical systems, any lens or mirror (e.g. a camera lens or the lens in the human eye) will make an image in which light from each point in the object is spread out over a certain region surrounding the point that is supposed to be (according to geometric optics) its image point. This causes a certain amount of blurring in the image.
Mathematically, the angular resolution of any lens is thus diffraction limited by the following relation.
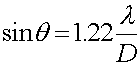
where D is the diameter of the lens and l is the wavelength. The factor 1.22 is a tradition based on a detailed calcultion of the exact position of the first dark ring in the diffraction pattern. In applications, the relevant angles are very small, so one can replace sinq by q, provided that q is measured in radians
The diffraction limit is a fundamental limitation on the quality of the image, which applies no matter how well the lens is designed or manufactured. It implies that lenses or mirrors used to see very fine details must have relatively large diameters. In the case of microscopes, some people use "oil immersion" lenses: having a layer of oil in contact with the lens reduces the wavelength of the light due to its index of refraction, and thus allows for better resolution with a given diameter D. To see even finer detail, one can use a smaller wavelength by using an electron beam instead of light. (The wave effects of electrons will be studied later in the Quantum Mechanics portion of the course.)