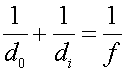with
di and do equal
to get 
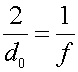
Examples for mirrors
Example #1
Problem:
a.) An image is located at exactly the same position as its object, for a mirror of focal length 6 cm. What is the object distance?
Solution:
Use the formula 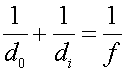with
di and do equal
to get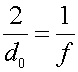
do = 12 cm
b.) If the height of the object is 4.5 mm, what is the height of the image?
Solution:
Use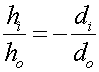 
to see that the image height
equals the object height.
hi = - 4.5 mm (inverted)
Example #2
Problem:
a.) A convex mirror has an object 14 cm from the mirror, and the image appears to be 7 cm behind the mirror. What is the focal length of the mirror?
Solution:
Use the formula 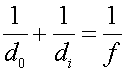with the image distance negative.
f = -14 cm
b.) If the object height is 8.0 mm, what is the height of the image?
Solution:
Use the formula 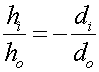with the image distance negative.
hi = 4.0 cm (upright)
Example #3
Problem:
Suppose one wishes to use a mirror as a projector, to illuminate a small object of height 1.0 cm, and display the image on a screen at a size of 1.0 m where the distance to the screen is 4.0 m.a.) What kind of mirror should one use? (concave or convex)
concave
b
.) What should the focal length of the mirror be? Solution: First calculate the object distance via the magnification formula. One obtains: do = 4.0 cm. Next, calculate the focal length via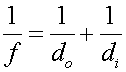
. Since di
is large compared to do, the focal length will be
approximately equal to do.
f
= 4.0 cm