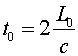
Length contraction
Moving objects appear shorter in the dimension parallel to their velocity, again by the factor g introduced previously. To derive the contraction we again consider a light clock; only in this case let the clock be on its side so the motion of the light pulse is parallel to the clock's velocity. If the clock has length L0 in its rest frame, the time for light to bounce from one side of the clock and back is:
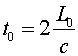
However to an observer who sees the clock pass at velocity v, the light takes more time to traverse the length of the clock when the pulse is traveling in the same direction as the clock, and it takes less time for the return trip.
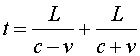
We know from the time dilation that
![]()
The above three equations can be used to eliminate t and t0 to obtain the result
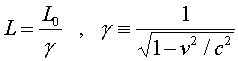
Thus moving meter sticks and all other moving objects appear shorter along their direction of motion. Like the time dilation effect, this happens as a result of the nature of space and time. It occurs equally for all objects, independent of what they are made of; it is not caused by forces, since as you well know, the force is zero when the velocity is constant.