 The formula for the impedance of an
LRC circuit can be derived as follows. This derivation is not required
for Physics 232.
The formula for the impedance of an
LRC circuit can be derived as follows. This derivation is not required
for Physics 232.
Derivation of Impedance
 The formula for the impedance of an
LRC circuit can be derived as follows. This derivation is not required
for Physics 232.
The formula for the impedance of an
LRC circuit can be derived as follows. This derivation is not required
for Physics 232.
Impedance is defined as the AC analog of resistance: it relates the rms current to the rms voltage of the source by
![]()
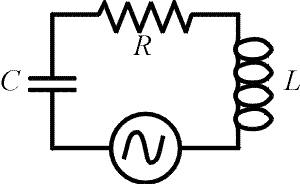
In the circuit on the right, Kirchhoff's laws require that the sum of the voltage drops across the three elements equals the voltage of the source at all times. Our goal is to write the sum of these three voltage drops in terms of the current. If the current behaves as
![]()
the voltage drops across the capacitor and inductor can be written as cosines since displacing a sine function by 90 degrees transforms the function into a cosine. With calculus, one would realize the voltage drops across the inductor and capacitor would have a cosine dependence because they are related by derivatives to the current.
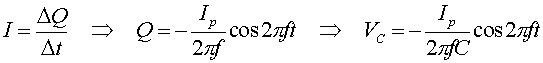
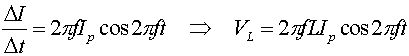
We can add up the voltages to get:
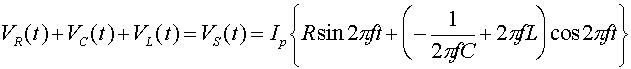
Using double-angle formulas from trigonometry, you can rewrite this as
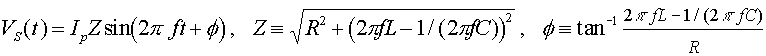
The gives the impedance Z. It also gives the phase difference f between the current and the voltage of the source.