RMS: what it means
An AC = "Alternating Current" circuit has a current that varies with time as a sine (or cosine) wave.
![]()
The peak current Ip is one way
to characterize the strength of that current. But a more standard way
is to use the r.m.s. (root-mean-square) value defined by
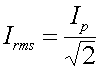 .
.
The r.m.s. value is a kind of average, as the word "mean" in the name root-mean-square implies. If you take the average over time of the square of the current, you get the square of the peak current times the average of the sine function squared, which is equal to 1/2. Hence the average over time of the square of the current is equal to the square of the rms current.
RMS quantities are particularly useful for calculating the power dissipated in a resistor. The same formulas that you learned for DC circuits (those with batteries)
P = I V, P = I2 R, P = V2 / R
tell the power at any given instant of time. (The power varies with time because I and V do.) The average power is also given by these same formulas, provided that you use the rms values for I and V.
When one refers to the 110 V or 120 V electrical outlets that are standard in American homes, the voltage being quoted is the r.m.s. value. The peak values are are larger by a factor of sqrt(2), i.e., 156V -- 170V.