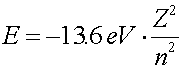
Many-electron atoms
A second electron added to a hydrogen atom will see both the charge of the proton as well as the charge of the electron that is already there. A second electron would be slightly bound (H+ ion), but you obviously cannot keep adding electrons indefinitely because the electrons repel each other. In fact, the largest number of electrons that can be bound to a single proton is two. Heavier nuclei, which have a larger number of protons and hence a larger positive charge Z e can bind many electrons.
For our purposes, we can talk about the energy levels of electrons in atoms without considering the effects of other electrons. The other electrons will adjust the energy levels somewhat, but for purposes of classification and insight, it is adequate to classify the orbitals as if the other electrons were not there except for their average effect on the charge. The key labels are the orbital and spin quantum numbers.
For one electron in the vicinity of a nucleus of charge Z, there are four quantum numbers that classify the electron, n, l, ml and ms. The first number n gives information about the energy of the orbital. Roughly, it describes the number of nodes in the wave function. The lowest energy level has n = 1, and the binding energy of the orbital falls inversely proportional to n2.
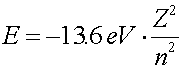
The second numbers l and ml give information about the angular momentum of the state. Both are always integers. The angular momentum ml is in integral units of h/(2p) but never exceeds + l and never goes below -l. For instance if l equals 3, ml can take on the seven values, -3,2,-1,0,1,2,3. The values of l can be from zero to n - 1. There are therefore (2l + 1) values of ml for each l. The last quantum number ms is always +1/2 or -1/2, so there are always exactly two such numbers.
Due to the screening of nuclear charge by the charges of the other electrons, the energies of various levels acquires a dependence on l as well as n. The levels are then denoted by n and l, and the two numbers ml and ms will be neglected except in knowing the number of different states that have a fixed n and l. That degeneracy is
![]()
The factor of two comes from the two values of ms and the other factor is for the different values of ml. Due to screenig, the lower values of l for a fixed n will have somewhat lower energy.
The electron shells for n < 5 are:
| n | l | degeneracy |
| 1 | 0 | 2 |
| 2 | 0 | 2 |
| 2 | 1 | 6 |
| 3 | 0 | 2 |
| 3 | 1 | 6 |
| 3 | 2 | 10 |
| 4 | 0 | 2 |
| 4 | 1 | 6 |
| 4 | 2 | 10 |
| 4 | 3 | 14 |
For instance, a neutral Iron atom has 26 electrons. One would fill states from the top of the table until 26 electrons were accounted for. If an atom had a given number of electrons Ne, one would fill the states from the top of the table until all Ne electrons were chosen.