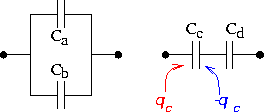
Capacitors in parallel and series
Here we discuss the effective capacitance of connecting two capacitors together. In the figure on the left the capacitors are connected in parallel, while in the right-hand figure the capacitors are connected in series.

First, let us consider the left-hand figure where the two capacitors are in parallel. The charge on the combined left-hand element is:
![]() ,
,
where V is the voltage across both elements. Remember that the voltage along a conductor does not change, and that a wire is a conductor, so both capacitors have the same voltage drop across them. From inspection of the equation above, one sees that the effective capacitance, C is:
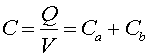
This makes sense because for parallel plate capacitors, the capacitance is e0A/d, and putting two identical capacitors side by side should look like one capacitor with double the area and therefore double the capacitance.
Next, consider the situation on the right, where the capacitors are in series. Remember that when we refer to the charge on a capacitor, it means the charge on one plate; the opposite charge appears on the other plate. Thus, the charge qd = qc.For two capacitors in series, the charges are identical, but the voltages are different. The sum of the voltage drops across the two capacitors must equal the net voltage drop V.
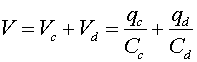
Using the fact that the effective charge Q on one plate of the combined system equals qc which equals qd, we see that
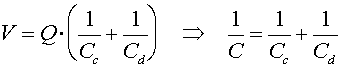
Thus we have found that