Problem:
Examples for electric field and equipotential lines
Example #1
Problem: 
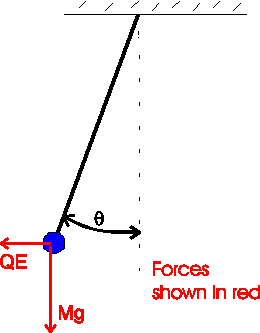
A charged ball of mass 6.0 g hangs from a string in a horizontal electric field of strength 200 V/m. The string makes an angle of 20 degrees with the vertical. What is the charge of the ball?
Solution:
The sum of the electric and gravitational forces must be along the direction of the
string. Thus,
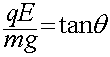
where q is the charge, E is the electric field, m is the mass and g is the acceleration of gravity, 9.8 m/s2. Solving for the charge q yields
q = 1.07E-4 C
Example #2
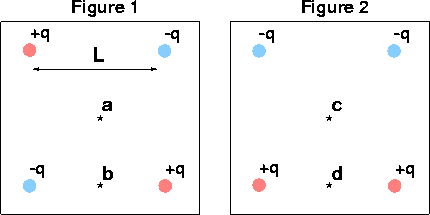
Problem:
Is the electric field zero at a,b,c,d?
yes,no,no,no
Is the electric potential zero at a,b,c,d?
yes,yes,yes,no
Example #3
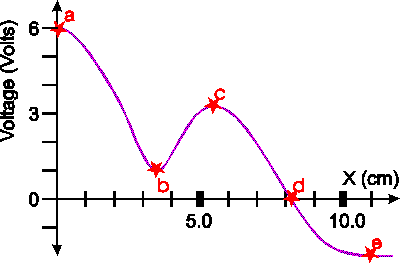
The graph shows the electrical potential as a function of distance along some particular direction in space. Name the points (a,b,c...) where
a.) The electric field is zero.
b.) The voltage is zero.
c.) What is the electric field at 'd'.
(The electric field is equal to the change in potential divided by the distance moved, i.e. the change in potential divided by the change in distance. This amounts to the derivative of of the potential with respect to distance -- which is easier to think about if you have studied enough calculus to be familiar with the concept of a derivitive!)
Answers:
a.) The E-field is zero where the slope is zero, a,b,c,e.
b.) The Potential is zero at d.
c.) The electric field is to the right (downhill points to the right) and the magnitude is given by the slope.
One must measure the slope as rise over run, which can be accomplished by drawing a line tangent to the purple curve at d. It appears that in 2.0 cm that the voltage would change the voltage by approximately 5 volts, thus the magnitude of the electric field is (5.0/2.0) (V/cm) which is
250 V/m
Example #4
![]()
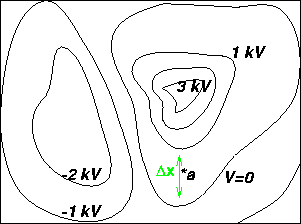 Problem:
Problem:
a.) What is the magnitude and direction of the electric field at a?
Solution:
The electric field is given by:
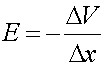
where ![]() is 1000 volts and
is 1000 volts and ![]() is the distance between the
two lines, which we measure to be 1.4 cm. Therefore E=1000/.014.
is the distance between the
two lines, which we measure to be 1.4 cm. Therefore E=1000/.014.
E = 7.1E4 (V/m)
b.) If a proton were released from rest at the V=0 equipotential line, what would its velocity be when it crossed the V=-1 kV line?
Solution:
Use conservation of energy. The kinetic energy gained by the proton is equal to its charge times the potential difference, KE = e*1000 Volts, where e is the charge of a proton, 1.6E-19 C. Setting the kinetic energy equal to mv2/2, one can solve for the velocity, v. (mass of proton = 1.67E-27 kg)
4.3E5 m/s