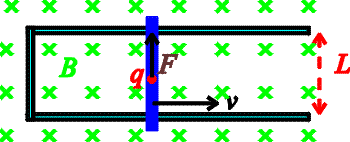
Motion-induced EMF
Let's look at a simple physical situation: a conducting metal bar (blue) of length L is moving to the right at velocity v through a constant magnetic field B that points into the page.

A charge q in the metal will feel a magnetic force
F = q v B. This force will have the same
effect as an electric force F = q E with
E = v B. Hence the magnetic force will act like
an electrical potential difference V = E L = v B L.
This potential difference, like that generated by a battery, is sometimes
called an "emf", and sometimes denoted by
![]() .
.
Now let the bar slide along conducting rails, as shown, to make a closed loop. The flux through the loop is B times the area A of the loop. The area is increasing as the bar slides to the right. Quantitatively, DA / D t = L v so general formula V = D F / Dt gives the same result
V = B v L
The induced voltage will cause a current to flow around the loop. The magnitude of the current will depend on the resistance of the bar and the rails. The direction of the current is counterclockwise, since positive charge flows upward in the bar as explained above. This direction can also be obtained by Lenz's Law: the induced current will generate a magnetic field that opposes the change in flux. In this case, the flux is increasing, so the induced current makes a field in the opposite direction to the one that is already there.
(This hypothetical situation was actually tried by NASA as a source of electrical power for earth satelites. The role of the rails was played by ions in the very thin outer atmosphere; the role of the sliding bar was played by a thin wire several miles long, which unfortunately broke during the experiment.)