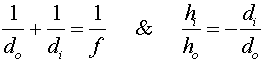
Formula review
The following two formulas apply to both mirrors and lenses:
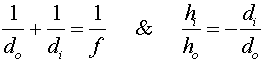
The greatest
difficulty is in remembering the signs of the variables.
I think the easiest way to do it is the following:
All of the possibilities are listed in the following table. I think this is an unnecessarily complicated way of summarizing the different cases; but some students prefer to have it stated this way:
focal length |
object distance |
image distance |
|
concave
|
positive |
positive |
positive, if on
the same side as object (real) |
convex
|
negative |
positive |
negative,as all
images are virtual |
converging
|
positive |
positive |
positive, if on
the opposite side as object (real) |
diverging
|
negative |
positive |
negative,as all
images are virtual |
Truths for both lenses and mirrors
Image distances are always negative for virtual images and positive for real images.
Object distances are always positive.
Real images are always inverted and virtual images are upright.