
Telescopes
Telescopes and microscopes both use two lenses to produce magnified images. The two lenses of a telescope are called the object lens and the eyepiece. Both are converging lenses, but the eyepiece has a much shorter focal length. The telescope is illustrated below.

The image produced by the object lens lies near the focal point of both lenses. This image then serves as the object for the eyepiece. The height, h', of that final image is given by
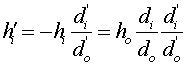
The second image is located at a distance di', which is far behind the lens. Given that the first image is at the focal point of both lenses, the above equation can be rewritten as
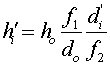
Both the distances in the above equation are very
large. However, it is the angular magnification that is relevant
for a telescope. The angle subtended by the original object is
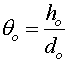 ,
while the angle subtended by the final image is
,
while the angle subtended by the final image is
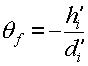 .
The ratio of the angles subtended by the final image and the original object
is the angular magnification.
.
The ratio of the angles subtended by the final image and the original object
is the angular magnification.
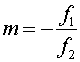
The final image seen in a telescope is inverted and appears larger by a factor of the ratio of the two focal lengths. To get a large magnification, the first lens must have a long focal length, and hence the telescope itself has to be rather long. In order to look at dim objects, such as far-away stars, the object lens must have a sufficiently large diameter to take in enough light to be seen (Power = Intensity*Area). This consideration also may force telescope designs to be large, and to favor the use of a mirror instead of a lens for the first element.