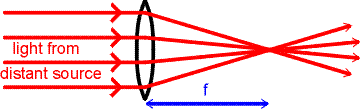
 A converging lens will focus light from a distant
source to the point called the focal point.
The focusing is illustrated in the figure on the right.
A converging lens will focus light from a distant
source to the point called the focal point.
The focusing is illustrated in the figure on the right.Focal lengths and focal points
Lenses can focus light and make images in a very similar way to mirrors. Lenses are either converging (convex on both sides, or concave on one side but more strongly convex on the other --- i.e., thicker in the center than at the edges) or diverging (concave on both sides, or concave on one side more strongly than convex on the other --- i.e., thinner in the center than at the edges). Both concave and convex lenses are used in a variety of optical instruments that will be studied in the next lecture.
As in the case of mirrors, there are three prototypical cases. The principal example is the camera lens -- a converging lens used to form a real image of an object that is farther away from the lens than the focal point. Equivalent examples are the lens in a slide or movie projector, which forms a real image on the screen; or a magnifying glass being used to form a real image of the sun on dry twigs to start a fire. In this case, like the real-image case for the mirror, the equation
1/di + 1/do = 1/f
has di, do, and f all positive. The magnification
M = -di / do
is therefore negative, so the real image is inverted.A second prototypical case is the magnifying glass used in the classic Sherlock Holmes style: a converging lens used to form a virtual image of an object that is held closer to the lens than the focal point. Here f is still positive (converging lens), but di is negative. Hence the magnification M is positive, so the virtual image is not inverted.
The third prototypical case is the peep-hole lens, a diverging lens used to make a virtual image that is smaller than the object. Here f is negative (diverging lens) and M is positive so the image is not inverted.
 A converging lens will focus light from a distant
source to the point called the focal point.
The focusing is illustrated in the figure on the right.
A converging lens will focus light from a distant
source to the point called the focal point.
The focusing is illustrated in the figure on the right. |
 Concave lenses spread light out rather than
bringing the rays together. The image from a concave lens is
therefore always virtual. A common example is the "peep-hole"
in a hotel room or apartment door. The focusing is illustrated in the figure on
the right. To an observer on the right side of the lens,
the light appears to come from the focal point on the
left side of the lens. The focal length of a concave lens
is assigned a negative number. Concave lenses spread light out rather than
bringing the rays together. The image from a concave lens is
therefore always virtual. A common example is the "peep-hole"
in a hotel room or apartment door. The focusing is illustrated in the figure on
the right. To an observer on the right side of the lens,
the light appears to come from the focal point on the
left side of the lens. The focal length of a concave lens
is assigned a negative number. |