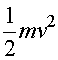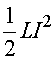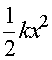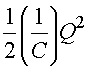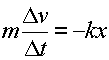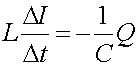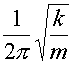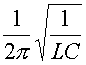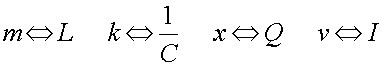LC circuits
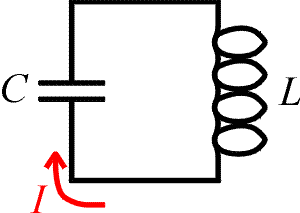An LC circuit is a closed loop with just two
elements: a capacitor and an inductor. It has a resonance property
like mechanical systems such as a pendulum or a mass on a spring: there is a
special frequency that it likes to oscillate at, and therefore responds
strongly to. LC circuits can be used to tune in to a
specific frequency, for example in the station selector of a radio or television.
In an LC circuit, electric charge oscillates back and forth just like the position of a mass on a spring oscillates. To demonstrate the analogy, we list several corresponding equations for a mechanical spring and an LC circuit.
mechanical spring |
LC circuit |
| position: x | charge: Q |
velocity:  |
current:  |
kinetic
energy:  |
inductor's
energy:  |
potential
energy:  |
capacitor's
energy:  |
Eq. of
motion:  |
Kirchhoff's
law:  |
frequency:  |
frequency:  |
The parameters that determine the motion of a spring are the mass m, spring constant k, the position x, and the velocity v which is the rate of change of x. The parameters that determine the behavior of an LC circuit are L, C, Q and I which is the rate of change of Q. Thus there is a one-to-one correspondence since the equations of motion are identical given the substitutions:
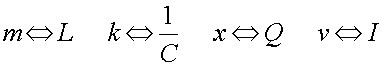
The characteristic frequency of an LC circuit is the frequency at which large amplitudes are built up when a driving force is applied at that frequency. A child on a swing will be sensitive to a pushing force which comes regularly with the natural frequency of the swing. A force that comes at a different frequency will not build up a large amplitude as it will often be pushing against the child's motion. The magic frequency is called the resonant frequency.