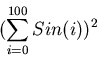Worksheet 1, PHY301 - Fall 2005
Due Sept 16, 2005 - three weeks

One way to begin learning C++ programming would be to study a bunch of simple working programs. If you choose that route, a suitable collection can be found at MSU CSE231

PROBLEMS

Problem 1. Write a C++ code that prints out your name.

Problem 2. Write a C++ code that calculates and prints out the following sum (where i is in radians)

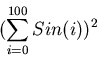$$(\sum_{i=0}^{100} Sin(i))^2$$ (1)

Check your result by doing the same calculation in Mathematica.

Problem 3. Write a C++ code that finds the integral of a function f(x) over the interval (a,b) using the simplest equally spaced Trapezoid rule. As an example use

$$\int_0^1 e^{-x^2} dx.$$ (2)

Calculate the integral above using Mathematica to check that you got it right.

Problem 4. Do the same, but use the integration method in which the interval is again divided into equal intervals, but the integrand is evaluated only at the centers of those intervals. Use equal weights. Again check the answer with Mathematica. (You will find that this simple method is actually somewhat more accurate than the trapezoidal method.)

Problem 5. Repeat problem 4, but this time make the integrand more challenging by inserting a singular factor 1/sqrt(x) in it. The integral remains finite and the method of problem 4 will still work, even though the trapezoidal rule method clearly fails by giving an infinite answer.

Problem 6. Plot the value obtained for the integral as a function of the number of ``mesh points'' used to evaluate it, using the graphics utility xmgrace. To do this, you will have to add a loop to your program to make it try a variety of mesh point numbers.

To use xmgrace, you first create a two-column file of the x and y values to be plotted. If that file is called foo.dat, the command xmgrace foo.dat should produce the plot. Alternatively, you can fire up the graphics program with the command xmgrace and use the drop-down menus in the following sequence: ``data", ``import", ``ASCII"; then pick your file. Either way, you can then change the appearance of the plot using the drop-down menu options under ``plot".

Info on xmgrace: http://plasma-gate.weizmann.ac.il/Grace/ (Note, to look at www sites outside MSU, the web browsers in BPS 1240 must be set to use a proxy server.)

Problem 7 (Optional). If you wish to carry out a more advanced study, you could determine empirically in what manner the integration error goes to zero as the number of intervals increases, and see if you can understand that theoretically. (Hint: the error falls as a power of 1/Nintervals; the power is different for the singular and non-singular cases.)

How to compile and run a C++ code in 1240 BPS

To compile:
g++   -o   file.exe   file.cpp

To compile and get possibly useful warning messages:
g++   -Wall   -o   file.exe   file.cpp

To execute:
./file.exe

If you prefer, it is also possible to compile using simply
g++   file.cpp
after which you run using
./a.out