BEAM 3 – SIMULATION PROGRAM FOR LIGHT TRACING IN OPTICAL SYSTEMS

These notes do not replace the manual!

What do you need:

A NEW or SAVED

a) OPTICS file (for example NEWTON.OPT): Contains a list of all optical surfaces in the system to be studied. The surface must be listed in the order in which the rays will encounter them.

b) RAY file (for example NEWTON.RAY): Contains a list of start positions and directions of light rays

c) MEDIA file (for example GLASS.MED): Contains a table of refractive indices of different materials for various wavelengths. This file needs only to be opened if your optics file lists material types instead of refraction indices.

Save your files in your own directory under C:\Documents and Settings\1235-xx\Desktop\PHY170-fall-student\, where

1235-xx is the name of the computer you are using. There you will also find a duplicate copy of the BEAM3 directory, so you can easily find BEAM3 files as well as your own files.

Run Functions:

Run:Layout command – performs a ray trace and creates a layout diagram of system. Refractive materials are drawn shaded, and rays according to color codes in ray table. (*most likely useful to visualize ray path)

HOT KEYS:

F5	Zoom In (Vertical)	Ctrl & F6	move between optics, ray and layout screen
F6	Zoom Out (Vertical)	Ctrl &C	copy to clipboard
F7	Zoom In (All, coarse adjustment)	Ctrl & V	paste from clipboard
F8	Zoom Out (All, coarse adjustment)	Ctrl & X	cut to clipboard
“+”	Zoom In (All, fine adjustment)
“-”	Zoom Out (All, fine adjustment)

Run:InOut command – performs a ray trace and fills in any output data requested by column header name in the RAY table. If a “notes” column is allocated then an abbreviated note will be filled describing the final fate of each ray.

Run:Plot command – performs a ray trace and then constructs a scatter plot of any two variables: position, direction, optical path length etc at any surfaces, versus any other such variable at any surface.

Run:Autoadjust – performs a ray trace and dynamically varies those optics and ray start parameters that have been tagged with question marks (?). Can be stopped at any time and often used to focus.

Coordinate System

· Describe each optical surface location by means of the coordinates (X,Y,Z in the lab frame) of its vertex (pt. at which the surface cuts its own axis)

· Orientation of surface can be changed by

v TILT – pivots a surface around its +x axis

v PITCH – rotates around its +y axis

v ROLL – rotates around the +z axis (see page #32 of manual for visual representation)

Ray Coordinates

Three parameters describe the direction of each ray segment: U, V, and W which are the X, Y, and Z components of the unit-length vector that points in the direction of the ray. In all cases you need to have U² + V² + W² = 1.00. They are referred to as direction cosines due to the fact that each is the cosine of the angle between the ray and its coordinate axis. (U=cos a, V=cos b W=cos g where a, b, g are the angles between the rays and the x, y and z axes respectively)

Example

· A ray headed in the +z direction has U=0, V=0, and W=1.

· A ray headed in the –y direction has U=0, V=-1, and W=0.

· A ray headed 37 degrees away from the +z direction towards the +x direction has U=0.6, V=0 and W=0.8.

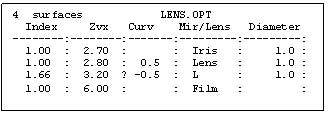Optics Tables: Example:

Text files organized on a line-by-line basis and can be edited with some useful functions (see page #77). You need three components to an optics file:

v title line (to include the # of surfaces and an appropriate title and maybe other relevant info.)

v column header line (fully programmable with a listing included on page )

v ruler line (set the demarcation of the fields specifying how many digits are allocated to each column.)

Information in the MIRROR/LENS surface identity column tells the program how to calculate ray direction changes at each surface.

Surface TYPES:

M, m	Mirror surface	G	Transmission grating
L, l, blank	Lens surface (default)	g	Reflection grating
I, I	Iris	tir	Total internal reflector
Fresnel	Fresnel mirror	retro	Retroreflector
fresnel	Fresnel lens	other	Phantom: no ray deviation

The column headers can be customized to fit the specific simulation (detailed description of each is found on page # 38)

Tags – character appearing exactly beneath a field separator. (?,>,<, etc. see page #45 for details) which may be used in flagging critical parameters to be used with AUTOADJUST in making slight changes to these parameters when needed.

Surface Profiles

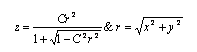Each spherical surface is described by a numerical value in the curvature (C) column whose value is the reciprocal of the radius of curvature (R), and zero if the surface is flat (i.e. C=1/R). It is positive if the surface curves towards the +z direction or negative for –z direction.

In local coordinates, the equation of a spherical surface with curvature C is:

Here r represents the radial distance from the axis of the surface.

A SHAPE column can be added to an optics table to specify the conic class of aspheric surfaces.

Surface SHAPES:

shape < 0.0 hyperboloid

shape = 0.0 paraboloid

0 < shape < 1.0 prolate ellipsoid

shape = 1.0 sphere

shape > 1.0 oblate ellipsoid