PHYSICS 321 - Classical Mechanics I

Spring 2010

Homework Set #11 (due 4/28/10)

1. Do problem 7-6 in Thornton and Marion without using the Lagrangian metod. Here is how to do it:

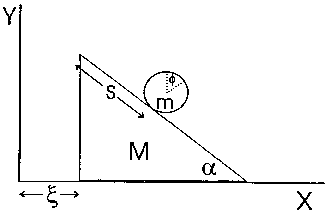
(a) Write down the total kinetic energy T of the hoop and incline plane, using the x and y coordinates of the hoop and the angle φ. Don't forget that the hoop has both rotational and translational kinetic energy. Use I=mR² for the hoop.

(b) Now switch to the coordinates s and ξ, and eliminate x, y, and φ from your expression for T. (What is the relationship between s and φ?)

(c) Write down the potential energy U for the system. (It does not matter where you take the origin - adding a constant does not change the physics.)

(d) Write down an equation describing coservation energy. Assume the hoop and incline start from rest when s=0.

(e) The horizontal component of linear momentum of the (hoop+incline) system is also conserved, because there are no horizontal forces acting on the system. (The plane slides without friction along the table.) Write down an equation describing this coservation law.

(f) Now write down the acceleration of the incline plane, ξ-ddot, and the acceleration of the hoop with respect to the plane, s-ddot. You will need to combine everything and take some time derivatives to get these.

2. Now do Thornton and Marion problem 7-6 using the Lagrangian method. Some of the work, such as calculating T and U, you have already done in the previous problem. So you just need to write down the Lagrangian and Lagrange equations in terms of the coordinates s and ξ. Then you can solve for s-ddot and ξ-ddot uncoupling the equations.

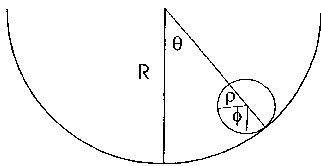
3. Marion & Thornton, problem 7-3. You may use either the Lagrangian method or the Conservation of Energy method. In either case, the constraint of no slipping gives you a relationship between the two angles θ and φ. Use that to eliminate φ, so you end up with a differential equation for the variable θ. (Note that the distance of the center of the sphere to the center of the hollow cylinder is (R-ρ), rather than R.)

4. Marion & Thornton, problem 7-12. Do this problem using the Lagrangian method. (To use Newton's 2^nd Law, you might need to consider a non-inertial reference frame with rotating axes, which we have not discussed in this course.) Here are the steps you should follow:

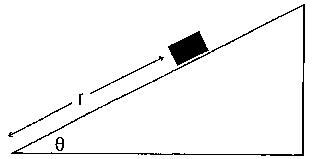
(a) Write down the Lagrangian, using the variables r and θ. Now put in the explicit form for θ and θ-dot, so you are left with only the coordinate r.

(b) Lagrange's equation should give you an inhomogeneous differential equation for r. (You may recognize the loathsome "centrifugal force" in this equation.)

(c) Now use all the tricks you learned about differential equations in Chapter 3. The general solution consists of the solution to the homogeneous equation, plus a particular solution to the inhomogeneous equation. For the particular solution, try r_p, = C sin(αt), and plug in to the D.E. to find the constant C.

(d) Now use the initial conditions to determine the two unknown constants in the homogeneous solution. Simplify the answer using cosh and sinh and you are all done.