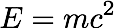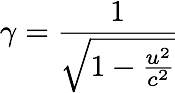I know what you're thinking: "I never had physics in High School, am I in trouble?" Having some physics under your belt will help, but not as much as you might suspect.
To those who have had physics: you'll feel superior to your colleagues for only a few weeks. ;-)
By that point we'll be flying to places you've not seen before!
You do need to be prepared for a little bit of math, but not what you think.
Math
We'll use mathematics in three ways: 1. math that you'll need to do in order to do the homework, 2. math that you'll need to read in order to follow an argument, and 3. math that we'll not derive but investigate.
1. Yes. Do Some Math
You might need to solve a simple equation for a single variable. Here's a famous one:
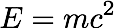
Can you solve for m? There's a lot of physics in that simple rearrangement. You'll be surprised that many of the most fundamental and mind-bending concepts in modern physics come from really pretty simple equations. How about the "doing" part. Well I'll simply give you a plot of that function and not ask you to actually mess with a calculation. Easy!
2. Yes. Read Some Math
Does that makes sense to you? "Read math"? Sure! Math is a language and reading it for understanding is a different kind of thing that having to come up with it out of your head in order to solve a problem. Any of you who have taken a foreign language can appreciate that. Isn't it easier to read a newspaper in French than to try to write an essay in French? If you've taken Latin, then I know you know what I mean.
So you'll encounter some mathematics in the lectures and the readings and you'll need to work out the meaning.
There's only one way to do that---which I do: Write. It. Out. I mean literally write what you see in your notes. Even if that means copying it down as you read it. Reading mathematics is a different kind of brain-work than reading text and it will go into your head better if it passes through your fingers. Trust me. Read with your pencil and sometimes copy symbols and equations verbatim.
3. Yes. Mess "inside" of equations
Sometimes we'll need some more complicated formulas but I don't want take you through a derivation or ask you to actually use the whole equation. But there is a story to tell by making some adjustments and predicting the outcomes.
Here's an example:
This is the "gamma function" (since the Greek symbol γ is called gamma):
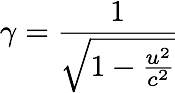
This is an important function in Einstein's Theory of Relativity and there are some simple things that we can do with it: first the reading part.
Q: What happens to this function when u becomes zero?
A: It becomes 1.
Q: What happens to this function when u becomes really tiny as compared c?
A: It gets really close to 1.
And that didn't require any real calculation...just some "reading" of the symbols.
In your head you'd be saying to yourself for the first question: "Lets see..if u becomes zero, then the stuff downstairs inside of the square root would be one minus zero, which is one. The square root of 1 is, well, 1. So the function gamma then itself becomes 1." Right? That's what happened in your head. I could hear it.
Q: How about if the quantity u becomes equal to c?
A: Can you see that this function becomes very large, indeed, infinity?
Your head is doing the same thing again.
Summary!
No difficult calculations. Just some "reading" of formulas and maybe looking at how they change (bigger, smaller, lots, little...) as things inside of them change. And if there's serious calculation to be done...well, I'll give you a graph to read the value.
By doing only this, we can do a lot of physics. Trust me. I'm a doctor.
Can't get better than that, can it?